Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T03:04:19.417Z Has data issue: false hasContentIssue false
  • English
  • Français

Subdiffusive behavior generated by irrational rotations

Published online by Cambridge University Press:  01 August 2009

F. HUVENEERS
F. HUVENEERS*
Affiliation:
UcL, FYMA, 2 Chemin du Cyclotron, B-1348 Louvain-la-Neuve, Belgium (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

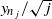We study asymptotic distributions of the sums yn(x)=∑ k=0n−1ψ(x+kα) with respect to the Lebesgue measure, where α∈ℝ−ℚ and where ψ is the 1-periodic function of bounded variation such that ψ(x)=1 if x∈[0,1/2[ and ψ(x)=−1 if x∈[1/2,1[. For every α∈ℝ−ℚ, we find a sequence (nj)j⊂ℕ such that is asymptotically normally distributed. For n≥1, let zn∈(ym)m≤n be such that ‖zn‖L2=max m≤n‖ym‖L2. If α is of constant type, we show that zn/‖zn‖L2 is also asymptotically normally distributed. We give a heuristic link with the theory of expanding maps of the interval.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 29 , Issue 4 , August 2009 , pp. 1217 - 1233
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Adamczewski, B.. Répartition des suites (nα)n∈ℕ et substitutions. Acta Arith. 112 (2004), 1–22.CrossRefGoogle Scholar
[2]Baladi, V.. Positive Transfer Operators and Decay of Correlations (Advanced Series in Nonlinear Dynamics, 16). World Scientific, River Edge, NJ, 2000.CrossRefGoogle Scholar
[3]Bricmont, J., Gawedzki, K. and Kupiainen, A.. KAM theorem and quantum field theory. Comm. Math. Phys. 201(3) (1999), 699–727.CrossRefGoogle Scholar
[4]Bunimovich, L. A. and Sinai, Ya. G.. Statistical properties of Lorentz gas with a periodic configuration of scatterers. Comm. Math. Phys. 72 (1981), 479–497.CrossRefGoogle Scholar
[5]Burton, R. and Denker, M.. On the central limit theorem for dynamical systems. Trans. Amer. Math. Soc. 302(2) (1987), 715–726.CrossRefGoogle Scholar
[6]De La Rue, T., Ladouceur, S., Peskir, G. and Weber, M.. On the central limit theorem for aperiodic dynamical systems and applications. Theory Probab. Math. Statist. 57 (1997), 140–159.Google Scholar
[7]Dettmann, C. P. and Cohen, E. G. D.. Microscopic chaos and diffusion. J. Stat. Phys. 101(3-4) (2000), 775–817.CrossRefGoogle Scholar
[8]Drmota, M. and Tichy, R. F.. Sequences, Discrepancies and Applications (Lecture Notes in Mathematics, 1651). Springer, Berlin, 1997.CrossRefGoogle Scholar
[9]Gaspard, P., Briggs, M. E., Francis, M. K., Sengers, J. V., Gammon, R. W., Dorfman, J. R. and Calabrese, R. V.. Experimental evidence for microscopic chaos. Nature 394 (1998), 865–868.CrossRefGoogle Scholar
[10]Hardy, G. H. and Wright, E. M.. An Introduction to the Theory of Numbers, 4th edn. Oxford University Press, Oxford, 1960.Google Scholar
[11]Herman, M. R.. Sur la conjugaison différentiable des difféomorphismes du cercle à des rotations. Publ. Math. Inst. Hautes Études Sci. 49 (1979), 5–233.CrossRefGoogle Scholar
[12]Hofbauer, F. and Keller, G.. Ergodic properties of invariant measures for piecewise monotonic transformations. Math. Z. 180 (1982), 119–140.CrossRefGoogle Scholar
[13]Kuipers, L. and Niederreiter, H.. Uniform Distribution of Sequences. Wiley, New York, 1974.Google Scholar
[14]Liardet, P. and Volný, D.. Sums of continuous and differentiable functions in dynamical systems. Israel J. Math. 98 (1997), 29–60.CrossRefGoogle Scholar