Article contents
Subdiagrams and invariant measures on Bratteli diagrams
Published online by Cambridge University Press: 12 May 2016
Abstract
We study ergodic finite and infinite measures defined on the path space 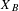 $X_{B}$ of a Bratteli diagram
$X_{B}$ of a Bratteli diagram 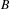 $B$ which are invariant with respect to the tail equivalence relation on
$B$ which are invariant with respect to the tail equivalence relation on 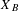 $X_{B}$. Our interest is focused on measures supported by vertex and edge subdiagrams of
$X_{B}$. Our interest is focused on measures supported by vertex and edge subdiagrams of 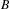 $B$. We give several criteria when a finite invariant measure defined on the path space of a subdiagram of
$B$. We give several criteria when a finite invariant measure defined on the path space of a subdiagram of 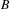 $B$ extends to a finite invariant measure on
$B$ extends to a finite invariant measure on 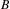 $B$. Given a finite ergodic measure on a Bratteli diagram
$B$. Given a finite ergodic measure on a Bratteli diagram 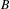 $B$ and a subdiagram
$B$ and a subdiagram 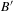 $B^{\prime }$ of
$B^{\prime }$ of 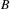 $B$, we find the necessary and sufficient conditions under which the measure of the path space
$B$, we find the necessary and sufficient conditions under which the measure of the path space 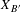 $X_{B^{\prime }}$ of
$X_{B^{\prime }}$ of  $B^{\prime }$ is positive. For a class of Bratteli diagrams of finite rank, we determine when they have maximal possible number of ergodic invariant measures. The case of diagrams of rank two is completely studied. We also include an example which explicitly illustrates the proven results.
$B^{\prime }$ is positive. For a class of Bratteli diagrams of finite rank, we determine when they have maximal possible number of ergodic invariant measures. The case of diagrams of rank two is completely studied. We also include an example which explicitly illustrates the proven results.
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2016
References
- 4
- Cited by


