Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T03:39:41.492Z Has data issue: false hasContentIssue false
  • English
  • Français

Subadditive mean ergodic theorems

Published online by Cambridge University Press:  19 September 2008

Y. Derriennic  and
U. Krengel
Y. Derriennic
Affiliation:
Département de Mathématiques, Université de Bretagne Occidentale, Brest, France
U. Krengel*
Affiliation:
Institüt für Mathematische Statistik, Göttingen, West Germany
*
†Dr U. Krengel, Institüt für Mathematische Statistik, Lotzestrasse 13, 3400 Göttingen, West Germany.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The authors investigate which results of the classical mean ergodic theory for bounded linear operators in Banach spaces have analogues for subadditive sequences (Fn) in a Banach lattice B. A sequence (Fn) is subadditive for a positive contraction T in B if Fn+k ≤ Fn + TnFk (n, k ≥ 1). For example, von Neumann's mean ergodic theorem fails to extend to the general subadditive case, but it extends to the non-negative subadditive case. 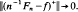It is shown that the existence of a weak cluster point f = Tf for (n−1Fn) implies In Lp (1 ≤ p < ∞) the existence of a weak cluster point for non-negative (n−1Fn) is equivalent with norm convergence. If T is an isometry in Lp (1 < p < ∞) and sup 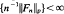then n−1Fn converges weakly. If T in L1 has a strictly positive fixed point and sup 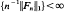then n−1Fn converges strongly. Most results are proved even in the d-parameter case.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 1 , Issue 1 , March 1981 , pp. 33 - 48
Copyright
Copyright © Cambridge University Press 1981

References

REFERENCES

[1]Akcoglu, M. A.. A pointwise ergodic theorem in Lp-spaces. Can. J. Math. 27 (1975), 1075–1082.CrossRefGoogle Scholar
[2]Akcoglu, M. A. & Krengel, U.. Ergodic theorems for super-additive processes. j. Reine u. Ang. Math. (in the press).Google Scholar
[3]Akcoglu, M. A. & Sucheston, L.. On convergence of iterates of positive contractions in Lp-spaces. J. Approx. Theory 13 (1975), 348–362.CrossRefGoogle Scholar
[4]Akcoglu, M. A. & Sucheston, L.. A ratio ergodic theorem for super-additive processes. Z. Wahrscheinlichkeitstheorie verw. Geb. 44 (1978), 269–278.CrossRefGoogle Scholar
[5]Birkhoff, G.. Lattice Theory. Amer. Math. Soc. Coll. Publ. XXV: Providence, R.I., 1940.Google Scholar
[6]Brunel, A.. Théorème ergodique ponctuel pour un semigroupe commutatif finiment engendré de contractions de L1. Ann. Inst. Henri Poincaré 9 (1973), 327–343.Google Scholar
[7]Denker, M., Grillenberger, C. and Sigmund, K.. Ergodic Theory on Compact Spaces. Springer Lecture Notes in Math. no. 527. Springer: Berlin, 1976.CrossRefGoogle Scholar
[8]Dunford, N. & Schwartz, J. T.. Linear Operators Vol. 1. Interscience Publ.: New York, 1958.Google Scholar
[9]Eberlein, W. F.. Abstract ergodic theorems and weak almost periodic functions. Trans. Amer. Math. Soc. 67 (1949), 217–240.CrossRefGoogle Scholar
[10]Fava, N. A.. Weak type inequalities for product operators. Studia Math. 42 (1972), 271–288.CrossRefGoogle Scholar
[11]Ghoussoub, N. & Steele, J. M.. Vector valued subadditive processes and applications in probability. Ann. Prob. 8 (1980), 83–95.CrossRefGoogle Scholar
[12]Heinich, H.. Convergence of positive submartingales in a Banach lattice. C. R. Acad. Sci. (Paris) Sec. A 286 (1978), 279–280.Google Scholar
[13]Kingman, J. F. C.. Subadditive ergodic theory. Ann. Prob. 1 (1973), 883–905.CrossRefGoogle Scholar
[14]Schaefer, H. H.. Banach Lattices and Positive Operators. Springer: New York, 1975.Google Scholar
[15]Smythe, R. T.. Multiparameter subadditive processes. Ann. Prob. 4 (1976), 772–782.CrossRefGoogle Scholar