Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T01:25:24.877Z Has data issue: false hasContentIssue false
  • English
  • Français

A strongly irreducible affine iterated function system with two invariant measures of maximal dimension

Part of: Classical measure theory Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  30 October 2020

IAN D. MORRIS  and
CAGRI SERT Open the ORCID record for CAGRI SERT [Opens in a new window]
IAN D. MORRIS
Affiliation:
School of Mathematical Sciences, Queen Mary, University of London, Mile End Road, London, E1 4NS, UK (e-mail: [email protected])
CAGRI SERT*
Affiliation:
Department Mathematik, ETH Zürich, Rämistrasse 101, 8092, Zürich, Switzerland
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A classical theorem of Hutchinson asserts that if an iterated function system acts on 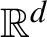$\mathbb {R}^{d}$ by similitudes and satisfies the open set condition then it admits a unique self-similar measure with Hausdorff dimension equal to the dimension of the attractor. In the class of measures on the attractor, which arise as the projections of shift-invariant measures on the coding space, this self-similar measure is the unique measure of maximal dimension. 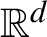In the context of affine iterated function systems it is known that there may be multiple shift-invariant measures of maximal dimension if the linear parts of the affinities share a common invariant subspace, or more generally if they preserve a finite union of proper subspaces of $\mathbb {R}^{d}$ . In this paper we give an example where multiple invariant measures of maximal dimension exist even though the linear parts of the affinities do not preserve a finite union of proper subspaces.

Keywords

self-affine setiterated function systemequilibrium statenon-conformal repellersubadditive thermodynamic formalism

MSC classification

Primary: 28A80: Fractals
Secondary: 37D35: Thermodynamic formalism, variational principles, equilibrium states
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 11 , November 2021 , pp. 3417 - 3438
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bárány, B., Hochman, M. and Rapaport, A.. Hausdorff dimension of planar self-affine sets and measures. Invent. Math. 216(3) (2019), 601–659.CrossRefGoogle Scholar
Barral, J. and Feng, D.-J.. Non-uniqueness of ergodic measures with full Hausdorff dimensions on a Gatzouras-Lalley carpet. Nonlinearity 24(9) (2011), 2563–2567.CrossRefGoogle Scholar
Benoist, Y.. Propriétés asymptotiques des groupes linéaires. Geom. Funct. Anal. 7(1) (1997), 1–47.CrossRefGoogle Scholar
Bochi, J. and Morris, I. D.. Equilibrium states of generalised singular value potentials and applications to affine iterated function systems. Geom. Funct. Anal. 28(4) (2018), 995–1028.CrossRefGoogle Scholar
Breuillard, E. and Sert, C.. The joint spectrum. Preprint, 2018, arXiv:1809.02404. J. London Math. Soc. to appear.Google Scholar
Cao, Y.-L., Feng, D.-J. and Huang, W.. The thermodynamic formalism for sub-additive potentials. Discrete Contin. Dyn. Syst. 20(3) (2008), 639–657.CrossRefGoogle Scholar
Das, T. and Simmons, D.. The Hausdorff and dynamical dimensions of self-affine sponges: a dimension gap result. Invent. Math. 210(1) (2017), 85–134.CrossRefGoogle ScholarPubMed
Dieudonné, J.. On the Automorphisms of the Classical Groups. With a Supplement by Loo-Keng Hua (Memoirs of the American Mathematical Society, 2) American Mathematical Society, Providence, RI, 1951.CrossRefGoogle Scholar
Falconer, K.. Techniques in Fractal Geometry. John Wiley & Sons, Ltd., Chichester, UK, 1997.Google Scholar
Falconer, K. J.. The Hausdorff dimension of self-affine fractals. Math. Proc. Cambridge Philos. Soc. 103(2) (1988), 339–350.CrossRefGoogle Scholar
Feng, D.-J.. Equilibrium states for factor maps between subshifts. Adv. Math. 226(3) (2011), 2470–2502.CrossRefGoogle Scholar
Feng, D.-J.. Dimension of invariant measures for affine iterated function systems. Preprint, 2019, arXiv:1901.01691.Google Scholar
Feng, D.-J. and Käenmäki, A.. Equilibrium states of the pressure function for products of matrices. Discrete Contin. Dyn. Syst. 30(3) (2011), 699–708.CrossRefGoogle Scholar
Gatzouras, D. and Peres, Y.. Invariant measures of full dimension for some expanding maps. Ergod. Th. & Dynam. Sys. 17(1) (1997), 147–167.CrossRefGoogle Scholar
Horn, R. A. and Johnson, C. R.. Topics in Matrix Analysis. Cambridge University Press, Cambridge, UK, 1994. Corrected reprint of the 1991 original.Google Scholar
Hutchinson, J. E.. Fractals and self-similarity. Indiana Univ. Math. J. 30(5) (1981), 713–747.CrossRefGoogle Scholar
Järvenpää, E., Järvenpää, M., Li, B. and Stenflo, O.. Random affine code tree fractals and Falconer-Sloan condition. Ergod. Th. & Dynam. Sys. 36(5) (2016), 1516–1533.CrossRefGoogle Scholar
Jordan, T., Pollicott, M. and Simon, K.. Hausdorff dimension for randomly perturbed self affine attractors. Comm. Math. Phys. 270(2) (2007), 519–544.CrossRefGoogle Scholar
Käenmäki, A.. On natural invariant measures on generalised iterated function systems. Ann. Acad. Sci. Fenn. Math. 29(2) (2004), 419–458.Google Scholar
Käenmäki, A. and Morris, I. D.. Structure of equilibrium states on self-affine sets and strict monotonicity of affinity dimension. Proc. Lond. Math. Soc. (3) 116(4) (2018), 929–956.CrossRefGoogle Scholar
Käenmäki, A. and Reeve, H. W. J.. Multifractal analysis of Birkhoff averages for typical infinitely generated self-affine sets. J. Fractal Geom. 1(1) (2014), 83–152.CrossRefGoogle Scholar
Käenmäki, A. and Vilppolainen, M.. Dimension and measures on sub-self-affine sets. Monatsh. Math. 161(3) (2010), 271–293.CrossRefGoogle Scholar
Morris, I. D.. Some observations on Käenmäki measures. Ann. Acad. Sci. Fenn. Math. 43(2) (2018), 945–960.CrossRefGoogle Scholar
Morris, I. D.. An explicit formula for the pressure of box-like affine iterated function systems. J. Fractal Geom. 6(2) (2019), 127–141.CrossRefGoogle Scholar
Morris, I. D. and Sert, C.. A converse statement to Hutchinson’s theorem and a dimension gap for self-affine measures. Preprint, 2019, arXiv:1909.08532.Google Scholar
Quint, J.-F.. Groupes de Schottky et comptage. Ann. Inst. Fourier (Grenoble) 55(2) (2005), 373–429.CrossRefGoogle Scholar
Zimmer, R. J.. Ergodic Theory and Semisimple Groups. Vol. 81. Springer Science & Business Media, Basel, 2013.Google Scholar