A strong submeasure on a compact metric space X is a sub-linear and bounded operator on the space of continuous functions on X. A strong submeasure is positive if it is non-decreasing. By the Hahn–Banach theorem, a positive strong submeasure is the supremum of a non-empty collection of measures whose masses are uniformly bounded from above. There are many natural examples of continuous maps of the form 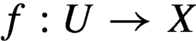$f:U\rightarrow X$ , where X is a compact metric space and 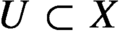$U\subset X$ is an open-dense subset, where f cannot extend to a reasonable function on X. We can mention cases such as transcendental maps of 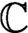$\mathbb {C}$ , meromorphic maps on compact complex varieties, or continuous self-maps 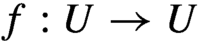$f:U\rightarrow U$ of a dense open subset $U\subset X$ where X is a compact metric space. For the aforementioned mentioned the use of measures is not sufficient to establish the basic properties of ergodic theory, such as the existence of invariant measures or a reasonable definition of measure-theoretic entropy and topological entropy. In this paper we show that strong submeasures can be used to completely resolve the issue and establish these basic properties. In another paper we apply strong submeasures to the intersection of positive closed 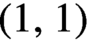$(1,1)$ currents on compact Kähler manifolds.