Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T10:58:40.981Z Has data issue: false hasContentIssue false
  • English
  • Français

Statistics and compression of scl

Published online by Cambridge University Press:  17 January 2014

DANNY CALEGARI  and
JOSEPH MAHER
DANNY CALEGARI
Affiliation:
University of Chicago, Chicago, IL 60637, USA email [email protected]
JOSEPH MAHER
Affiliation:
Department of Mathematics, CUNY College of Staten Island, Staten Island, NY 10314, USA and Department of Mathematics, CUNY Graduate Center, NY 10016, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We obtain sharp estimates on the growth rate of stable commutator length on random (geodesic) words, and on random walks, in hyperbolic groups and groups acting non-degenerately on hyperbolic spaces. In either case, we show that with high probability stable commutator length of an element of length $n$ is of order 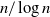$n/ \log n$. This establishes quantitative refinements of qualitative results of Bestvina and Fujiwara and others on the infinite dimensionality of two-dimensional bounded cohomology in groups acting suitably on hyperbolic spaces, in the sense that we can control the geometry of the unit balls in these normed vector spaces (or rather, in random subspaces of their normed duals). As a corollary of our methods, we show that an element obtained by random walk of length $n$ in a mapping class group cannot be written as a product of fewer than 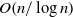$O(n/ \log n)$ reducible elements, with probability going to 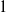$1$ as $n$ goes to infinity. We also show that the translation length on the complex of free factors of a random walk of length $n$ on the outer automorphism group of a free group grows linearly in $n$.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 1 , February 2015 , pp. 64 - 110
Copyright
©  D. Calegari & J. Maher 2014. Published by Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barvinok, A.. Integer Points in Polyhedra (Zurich Lectures in Advanced Mathematics). European Mathematical Society, Zürich, 2008.Google Scholar
Bavard, C.. Longueur stable des commutateurs. Enseign. Math. (2) 37 (1991), 109–150.Google Scholar
Bestvina, M. and Feighn, M.. A hyperbolic $\mathrm{Out} ({F}_{n} )$-complex. Groups Geom. Dyn. 4 (1) (2010), 31–58.Google Scholar
Bestvina, M. and Feighn, M.. Hyperbolicity of the complex of free factors. Preprint, 2001, arXiv:1107.3308.Google Scholar
Bestvina, M. and Fujiwara, K.. Bounded cohomology of subgroups of mapping class groups. Geom. Topol. 6 (2002), 69–89.Google Scholar
Björklund, M. and Hartnick, T.. Biharmonic functions on groups and limit theorems for quasimorphisms along random walks. Geom. Topol. 15 (1) (2011), 123–143.Google Scholar
Bowditch, B.. Tight geodesics in the curve complex. Invent. Math. 171 (2) (2008), 281–300.Google Scholar
Bridson, M. and Haefliger, A.. Metric Spaces of Non-positive Curvature (Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 319). Springer, Berlin, 1999.CrossRefGoogle Scholar
Brooks, R.. Some remarks on bounded cohomology. Riemann Surfaces and Related topics: Proceedings of the 1978 Stony Brook Conference (SUNY, Stony Brook, NY, 1978) (Annals of Mathematics Studies, 97). Princeton University Press, Princeton, NJ, 1981, pp. 53–63.Google Scholar
Burger, M. and Monod, N.. Bounded cohomology of lattices in higher rank Lie groups. J. Eur. Math. Soc. 1 (2) (1999), 199–235.Google Scholar
Calegari, D.. scl (MSJ Memoirs, 20). Mathematical Society of Japan, Tokyo, 2009.CrossRefGoogle Scholar
Calegari, D. and Fujiwara, K.. Combable functions, quasimorphisms and the central limit theorem. Ergod. Th. & Dynam. Sys. 30 (5) (2010), 1343–1369.Google Scholar
Calegari, D. and Walker, A.. Random rigidity in the free group. Preprint, arXiv:1104.1768, Geom. Topol., to appear.Google Scholar
Cannon, J.. The combinatorial structure of cocompact discrete hyperbolic groups. Geom. Dedicata 16 (2) (1984), 123–148.Google Scholar
Cannon, J., Floyd, W. and Parry, W.. Introductory notes on Richard Thompson’s groups. Enseign. Math. (2) 42 (3–4) (1996), 215–256.Google Scholar
Coornaert, M.. Mesures de Patterson–Sullivan sur le bord d’un espace hyperbolique au sens de Gromov. Pacific J. Math. 159 (2) (1993), 241–270.CrossRefGoogle Scholar
Dinwoodie, I.. Expectations for nonreversible Markov chains. J. Math. Anal. Appl. 220 (1998), 585–596.CrossRefGoogle Scholar
Epstein, D., Cannon, J., Holt, D., Levy, S., Paterson, M. and Thurston, W.. Word Processing in Groups. Jones and Bartlett, Boston, MA, 1992.Google Scholar
Epstein, D. and Fujiwara, K.. The second bounded cohomology of word-hyperbolic groups. Topology 36 (6) (1997), 1275–1289.Google Scholar
Farb, B. and Masur, H.. Superrigidity and mapping class groups. Topology 37 (6) (1998), 1169–1176.Google Scholar
Fujiwara, K.. The second bounded cohomology of a group acting on a Gromov-hyperbolic space. Proc. Lond. Math. Soc. (3) 76 (1) (1998), 70–94.Google Scholar
Fujiwara, K.. Subgroups generated by two pseudo-Anosov elements in a mapping class group. I. Uniform exponential growth. Groups of Diffeomorphisms (Advanced Studies in Pure Mathematics, 52). Mathematical Society of Japan, Tokyo, 2008, pp. 283–296.Google Scholar
Furman, A.. Random Walks on Groups and Random Transformations (Handbook of Dynamical Systems, 1a). North-Holland, Amsterdam, 2002, pp. 931–1014.Google Scholar
Ghys, É.. Knots and Dynamics (International Congress of Mathematicians. 1). European Mathematical Society, Zürich, 2007, pp. 247–277.Google Scholar
Ghys, É. and Sergiescu, V.. Sur un groupe remarquable de difféomorphismes du cercle. Comment. Math. Helv. 62 (2) (1987), 185–239.Google Scholar
Gromov, M.. Volume and bounded cohomology. Publ. Math. Inst. Hautes Études Sci. 56 (1982), 5–99.Google Scholar
Gromov, M.. Hyperbolic Groups (Essays in Group Theory, MSRI Publication 8). Springer, New York, 1987, pp. 75–263.Google Scholar
Groves, D. and Manning, J.. Dehn filling in relatively hyperbolic groups. Israel J. Math. 168 (2008), 317–429.CrossRefGoogle Scholar
Hall, P. and Heyde, C.. Martingale Limit Theory and Its Application. Academic Press, New York, 1980.Google Scholar
Hamenstädt, U.. Lines of minima in outer space. Preprint, arXiv:0911.3620, Duke Math. J., to appear.Google Scholar
Handel, M. and Mosher, L.. The free splitting complex of a free group I: hyperbolicity. Preprint, 2011, arXiv:1111.1994.Google Scholar
Horsham, M. and Sharp, R.. Lengths, quasi-morphisms and statistics for free groups. Spectral Analysis in Geometry and Number Theory (Contemporary Mathematics, 484). American Mathematical Society, Providence, RI, 2009, pp. 219–237.Google Scholar
Kaimanovich, V.. The Poisson formula for groups with hyperbolic properties. Ann. of Math. (2) 152 (2000), 659–692.Google Scholar
Kaimanovich, V. and Masur, H.. The Poisson boundary of the mapping class group. Invent. Math. 125 (2) (1996), 221–264.Google Scholar
Kakutani, S.. Random ergodic theorems and Markoff processes with a stable distribution. Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability, 1950. University of California Press, Berkeley, CA, 1951, pp. 247–261.Google Scholar
Kowalski, E.. The Large Sieve and its Applications: Arithmetic Geometry, Random Walks and Discrete Groups (Cambridge Tracts in Mathematics, 175). Cambridge University Press, Cambridge, 2008.Google Scholar
Liehl, B.. Beschränkte Wortlänge in ${\mathrm{SL} }_{2} $. Math. Z. 186 (4) (1984), 509–524.Google Scholar
Maher, J.. Linear progress in the complex of curves. Trans. Amer. Math. Soc. 362 (6) (2010), 2963–2991.Google Scholar
Maher, J.. Random Heegaard splittings. J. Topol. 3 (4) (2010), 997–1025.Google Scholar
Maher, J.. Exponential decay in the mapping class group. J. Lond. Math. Soc. (2) 86 (2) (2012), 366–386.Google Scholar
Picaud, J.-C.. Cohomologie bornée des surfaces et courants géodésiques. Bull. Soc. Math. France 125 (1) (1997), 115–142.CrossRefGoogle Scholar
Ratner, M.. Markov partitions for Anosov flows on $n$-dimensional manifolds. Israel J. Math. 15 (1973), 92–114.Google Scholar
Rivin, I.. Walks on groups, counting reducible matrices, polynomials, and surface and free group automorphisms. Duke Math. J. 142 (2008), 353–379.Google Scholar
Rivin, I.. Growth in free groups (and other stories)—twelve years later. Illinois J. Math. 54 (1) (2010), 327–370.Google Scholar
Sharp, R.. Local limit theorems for free groups. Math. Ann. 321 (2001), 889–904.Google Scholar
Sisto, A.. Contracting elements and random walks. Preprint, 2011, arXiv:1112.2666.Google Scholar
Stroock, D.. Probability Theory, an Analytic View. Cambridge University Press, Cambridge, 1993.Google Scholar
Witte-Morris, D.. Bounded generation of $\mathrm{SL} (n, A)$ (after D. Carter, G. Keller, and E. Paige). New York J. Math. 13 (2007), 383–421.Google Scholar
Woess, W.. Random Walks on Infinite Graphs and Groups (Cambridge Tracts in Mathematics, 138). Cambridge University Press, Cambridge, 2000.CrossRefGoogle Scholar
Zhuang, D.. Irrational stable commutator length in finitely presented groups. J. Mod. Dyn. 2 (3) (2008), 499–507.Google Scholar