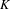Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T17:59:17.342Z Has data issue: false hasContentIssue false
  • English
  • Français

The stable algebra of a Wieler solenoid: inductive limits and $K$-theory

Part of: Selfadjoint operator algebras Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  10 April 2019

ROBIN J. DEELEY  and
ALLAN YASHINSKI
ROBIN J. DEELEY
Affiliation:
Department of Mathematics, University of Colorado Boulder, Campus Box 395, Boulder, CO80309-0395, USA email [email protected]
ALLAN YASHINSKI
Affiliation:
Department of Mathematics, University of Maryland, College Park, MD20742-4015, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Wieler has shown that every irreducible Smale space with totally disconnected stable sets is a solenoid (i.e., obtained via a stationary inverse limit construction). Using her construction, we show that the associated stable 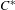$C^{\ast }$-algebra is the stationary inductive limit of a 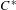$C^{\ast }$-stable Fell algebra that has a compact spectrum and trivial Dixmier–Douady invariant. This result applies in particular to Williams solenoids along with other examples. Beyond the structural implications of this inductive limit, one can use this result to, in principle, compute the 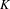$K$-theory of the stable $C^{\ast }$-algebra. A specific one-dimensional Smale space (the 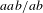$aab/ab$-solenoid) is considered as an illustrative running example throughout.

Keywords

operator algebrastopological dynamicsétale groupoidssolenoids

MSC classification

Primary: 46L80: $K$-theory and operator algebras (including cyclic theory) 37D20: Uniformly hyperbolic systems (expanding, Anosov, Axiom A, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 10 , October 2020 , pp. 2734 - 2768
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, J. E. and Putnam, I. F.. Topological invariants for substitution tilings and their associated C ∗ -algebras. Ergod. Th. & Dynam. Sys. 18(3) (1998), 509–537.CrossRefGoogle Scholar
Brown, L. G.. Stable isomorphism of hereditary subalgebras of C ∗ -algebras. Pacific J. Math. 71(2) (1977), 335–348.CrossRefGoogle Scholar
Burke, N. D. and Putnam, I. F.. Markov partitions and homology for n/m-solenoids. Ergod. Th. & Dynam. Sys. 37(3) (2017), 716–738.Google Scholar
Clark, L. O., an Huef, A. and Raeburn, I.. The equivalence relations of local homeomorphisms and Fell algebras. New York J. Math. 19 (2013), 367–394.Google Scholar
Deeley, R. J., Goffeng, M., Mesland, B. and Whittaker, M. F.. Wieler solenoids, Cuntz-Pimsner algebras and K-theory. Ergod. Th. & Dynam. Sys. 38(8) (2018), 2942–2988.Google Scholar
Deeley, R. J. and Strung, K. R.. Nuclear dimension and classification of C ∗ -algebras associated to Smale spaces. Trans. Amer. Math. Soc. 370(5) (2018), 3467–3485.Google Scholar
Gonçalves, D.. New C ∗ -algebras from substitution tilings. J. Operator Theory 57(2) (2007), 391–407.Google Scholar
Gonçalves, D.. On the K-theory of the stable C ∗ -algebras from substitution tilings. J. Funct. Anal. 260(4) (2011), 998–1019.Google Scholar
Gonçalves, D. and Ramirez-Solano, M.. On the $K$ -theory of $C^{\ast }$ -algebras for substitution tilings (a pedestrian version). Preprint, 2017, arXiv:1712.09551.Google Scholar
Guentner, E., Willett, R. and Yu, G.. Dynamic asymptotic dimension: relation to dynamics, topology, coarse geometry, and C ∗ -algebras. Math. Ann. 367(1-2) (2017), 785–829.Google Scholar
an Huef, A., Kumjian, A. and Sims, A.. A Dixmier-Douady theorem for Fell algebras. J. Funct. Anal. 260(5) (2011), 1543–1581.Google Scholar
Hjelmborg, J. v. B. and Rørdam, M.. On stability of C ∗ -algebras. J. Funct. Anal. 155(1) (1998), 153–170.CrossRefGoogle Scholar
Killough, D. B.. Ring structures on the $K$ -theory of $C$ *-algebras associated to smale spaces. PhD Thesis, University of Victoria, 2009.Google Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Mingo, J. A.. C ∗ -algebras associated with one-dimensional almost periodic tilings. Comm. Math. Phys. 183(2) (1997), 307–337.CrossRefGoogle Scholar
Putnam, I. F.. C ∗ -algebras from Smale spaces. Canad. J. Math. 48(1) (1996), 175–195.Google Scholar
Putnam, I. F.. A homology theory for Smale spaces. Mem. Amer. Math. Soc. 232(1094) (2014), viii+122.Google Scholar
Putnam, I. F. and Spielberg, J.. The structure of C ∗ -algebras associated with hyperbolic dynamical systems. J. Funct. Anal. 163(2) (1999), 279–299.CrossRefGoogle Scholar
Raeburn, I. and Williams, D. P.. Morita Equivalence and Continuous-trace C ∗ -Algebras (Mathematical Surveys and Monographs, 60) . American Mathematical Society, Providence, RI, 1998.CrossRefGoogle Scholar
Renault, J.. A Groupoid Approach to C ∗ -Algebras (Lecture Notes in Mathematics, 793) . Springer, Berlin, 1980.CrossRefGoogle Scholar
Renault, J.. The Radon-Nikodým problem for approximately proper equivalence relations. Ergod. Th. & Dynam. Sys. 25(5) (2005), 1643–1672.Google Scholar
Ruelle, D.. The mathematical structures of equilibrium statistical mechanics. Thermodynamic Formalism (Cambridge Mathematical Library) , 2nd edn. Cambridge University Press, Cambridge, 2004.Google Scholar
Smale, S.. Differentiable dynamical systems. Bull. Amer. Math. Soc. 73 (1967), 747–817.Google Scholar
Thomsen, K.. C ∗ -algebras of homoclinic and heteroclinic structure in expansive dynamics. Mem. Amer. Math. Soc. 206(970) (2010), x+122.Google Scholar
Thomsen, K.. The homoclinic and heteroclinic C ∗ -algebras of a generalized one-dimensional solenoid. Ergod. Th. & Dynam. Sys. 30(1) (2010), 263–308.Google Scholar
Wieler, S.. Smale spaces with totally disconnected local stable sets. PhD Thesis, University of Victoria, 2012.Google Scholar
Wieler, S.. Smale spaces via inverse limits. Ergod. Th. & Dynam. Sys. 34(6) (2014), 2066–2092.CrossRefGoogle Scholar
Williams, R. F.. Classification of one dimensional attractors. Global Analysis (Proc. Sympos. Pure Math., Vol. XIV, Berkeley, Calif., 1968). American Mathematical Society, Providence, RI, 1970, pp. 341–361.Google Scholar
Williams, R. F.. Expanding attractors. Publ. Math. Inst. Hautes Études Sci. 43 (1974), 169–203.CrossRefGoogle Scholar
Williamson, P.. Cuntz–Pimsner algebras associated with substitutuion tilings. PhD Thesis, Unviersity of Victoria, 2016.Google Scholar
Winter, W.. Structure of nuclear $C^{\ast }$ -algebras: from quasidiagonality to classification, and back again. Preprint, 2017, arXiv:1712.00247.Google Scholar
Winter, W. and Zacharias, J.. The nuclear dimension of C ∗ -algebras. Adv. Math. 224(2) (2010), 461–498.Google Scholar
Yi, I.. K-theory of C ∗ -algebras from one-dimensional generalized solenoids. J. Operator Theory 50(2) (2003), 283–295.Google Scholar