Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T01:05:39.716Z Has data issue: false hasContentIssue false
  • English
  • Français

Stabilizers of actions of lattices in products of groups

Published online by Cambridge University Press:  24 March 2016

DARREN CREUTZ
DARREN CREUTZ*
Affiliation:
Vanderbilt University, Nashville, TN, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that any ergodic non-atomic probability-preserving action of an irreducible lattice in a semisimple group, with at least one factor being connected and of higher-rank, is essentially free. This generalizes the result of Stuck and Zimmer [Stabilizers for ergodic actions of higher rank semisimple groups. Ann. of Math. (2)139(3) (1994), 723–747], who found that the same statement holds when the ambient group is a semisimple real Lie group and every simple factor is of higher-rank. We also prove a generalization of a result of Bader and Shalom [Factor and normal subgroup theorems for lattices in products of groups. Invent. Math.163(2) (2006), 415–454] by showing that any probability-preserving action of a product of simple groups, with at least one having property 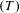$(T)$, which is ergodic for each simple subgroup, is either essentially free or essentially transitive. Our method involves the study of relatively contractive maps and the Howe–Moore property, rather than relying on algebraic properties of semisimple groups and Poisson boundaries, and introduces a generalization of the ergodic decomposition to invariant random subgroups, which is of independent interest.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 4 , June 2017 , pp. 1133 - 1186
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abert, M., Bergeron, N., Biringer, I., Gelander, T., Nikolov, N., Raimbault, J. and Samet, I.. On the growth of Betti numbers of locally symmetric spaces. C. R. Math. Acad. Sci. Paris 349(15–16) (2011), 831–835.CrossRefGoogle Scholar
Abert, M., Glasner, Y. and Virág, B.. Kesten’s theorem for invariant random subgroups. Duke Math. J. 163(3) (2014), 465–488.CrossRefGoogle Scholar
Adams, S., Elliott, G. and Giordano, T.. Amenable actions of groups. Trans. Amer. Math. Soc. 344(2) (1994), 803–822.CrossRefGoogle Scholar
Adams, S. and Stuck, G.. Splitting of nonnegatively curved leaves in minimal sets of foliations. Duke Math. J. 71(1) (1993), 71–92.CrossRefGoogle Scholar
Auslander, L. and Moore, C. C.. Unitary representations of solvable Lie groups. Mem. Amer. Math. Soc. 62 (1966), 66–77.Google Scholar
Bader, U. and Shalom, Y.. Factor and normal subgroup theorems for lattices in products of groups. Invent. Math. 163(2) (2006), 415–454.CrossRefGoogle Scholar
Bergeron, N. and Gaboriau, D.. Asymptotique des nombres de Betti, invariants ℓ 2 et laminations [Asymptotics of Betti numbers and ℓ 2 -invariants and laminations]. Comment. Math. Helv. 79(2) (2004), 362–395.CrossRefGoogle Scholar
Bowen, L.. Invariant random subgroups of the free group. Groups, Geom. Dynam., to appear, Preprint, 2012, arXiv:1204.5939.Google Scholar
Connes, A., Feldman, J. and Weiss, B.. An amenable equivalence relation is generated by a single transformation. Ergod. Th. & Dynam. Sys. 1(4) (1981), 431–450.CrossRefGoogle Scholar
Creutz, D.. Commensurated subgroups and the dynamics of group actions on quasi-invariant measure spaces. PhD Thesis, University of California, Los Angeles, 2011.Google Scholar
Creutz, D. and Peterson, J.. Stabilizers of ergodic actions of lattices and commensurators. Trans. Amer. Math. Soc., to appear, Preprint, 2013, arXiv:1303.3949.Google Scholar
Creutz, D. and Shalom, Y.. A normal subgroup theorem for commensurators of lattices. Groups, Geom. Dynam. 8 (2014), 1–22.Google Scholar
de Cornulier, Y.. On Haagerup and Kazhdan Properties. PhD Thesis, École Polytechnique Fédérale de Lausanne, 2005.Google Scholar
del Junco, A. and Rosenblatt, J.. Counterexamples in ergodic theory and number theory. Math. Ann. 245 (1979), 185–197.CrossRefGoogle Scholar
Dudko, A. and Medynets, K.. Finite factor representations of Higman–Thompson groups. Groups, Geom. Dynam. 8(2) (2014), 375–389.CrossRefGoogle Scholar
Furstenberg, H.. A Poisson formula for semi-simple Lie groups. Ann. of Math. (2) 77(2) (1963), 335–386.CrossRefGoogle Scholar
Furstenberg, H.. Poisson boundaries and envelopes of discrete groups. Bull. Amer. Math. Soc. 73(3) (1967), 350–356.CrossRefGoogle Scholar
Furstenberg, H.. Random walks and discrete subgroups of Lie groups. Adv. Probab. Relat. Top. 1 (1971), 1–63.Google Scholar
Furstenberg, H. and Glasner, E.. Stationary dynamical systems. Dynamical Numbers—Interplay Between Dynamical Systems and Number Theory (Contemporary Mathematics, 532) . American Mathematical Society, Providence, RI, 2010, pp. 1–28.Google Scholar
Glasner, E.. Ergodic Theory via Joinings (Mathematical Surveys and Monographs, 101) . American Mathematical Society, Providence, RI, 2003.CrossRefGoogle Scholar
Grigorchuk, R. I.. Some topics in the dynamics of group actions on rooted trees. Proc. Steklov Inst. Math. 273 (2011), 64–175.CrossRefGoogle Scholar
Grigorchuk, R. and Savchuk, D.. Self-similar groups acting essentially freely on the boundary of the binary rooted tree. Contemp. Math., to appear, Preprint, 2012, arXiv:1212.0605.Google Scholar
Hjorth, G. and Kechris, A.. Rigidity Theorems for Actions of Product Groups and Countable Equivalence Relations (Memoirs of the American Mathematical Society, 833) . American Mathematical Society, Providence, RI, 2005.CrossRefGoogle Scholar
Howe, R. E. and Moore, C. C.. Asymptotic properties of unitary representations. J. Funct. Anal. 32 (1979), 72–96.CrossRefGoogle Scholar
Jaworski, W.. Strongly approximately transitive group actions, the Choquet–Deny theorem, and polynomial growth. Pacific J. Math. 165(1) (1994), 115–129.CrossRefGoogle Scholar
Jaworski, W.. Strong approximate transitivity, polynomial growth, and spread out random walks on locally compact groups. Pacific J. Math. 170(2) (1995), 517–533.CrossRefGoogle Scholar
Kaimanovich, V. A.. Brownian motion on foliations: entropy, invariant measures, mixing. Funct. Anal. Appl. 22(4) (1988), 326–328.CrossRefGoogle Scholar
Kaimanovich, V. A.. Discretization of bounded harmonic functions on Riemannian manifolds and entropy. Proc. Int. Conf. on Potential Theory (1992), 213–223.CrossRefGoogle Scholar
Kechris, A. and Miller, B.. Topics in Orbit Equivalence. Springer, Berlin, 2004.CrossRefGoogle Scholar
Krasa, S.. Nonuniqueness of invariant means for amenable group actions. Monatsh. Math. 100 (1985), 121–125.CrossRefGoogle Scholar
Mackey, G.. Point realizations of transformation groups. Illinois J. Math. 6 (1962), 327–335.CrossRefGoogle Scholar
Mackey, G.. Ergodic theory and virtual groups. Ann. of Math. (2) 166 (1966), 187–207.CrossRefGoogle Scholar
Margulis, G.. Finiteness of quotient groups of discrete subgroups. Funktsional. Anal. i Prilozhen. 13 (1979), 28–39.CrossRefGoogle Scholar
Nevo, A. and Zimmer, R.. Homogenous projective factors for actions of semi-simple lie groups. Invent. Math. 138 (1999), 229–252.CrossRefGoogle Scholar
Ramsay, A.. Virtual groups and group actions. Adv. Math. 6 (1971), 253–322.CrossRefGoogle Scholar
Rosenblatt, J.. Uniqueness of invariant means for measure-preserving transformations. Trans. Amer. Math. Soc. 265(2) (1981), 623–636.CrossRefGoogle Scholar
Rothman, S.. The von Neumann kernel and minimally almost periodic groups. Trans. Amer. Math. Soc. 259 (1980), 401–421.CrossRefGoogle Scholar
Schmidt, K.. Asymptotic properties of unitary representations and mixing. Proc. Lond. Math. Soc. (3) 48(3) (1984), 445–460.CrossRefGoogle Scholar
Stuck, G. and Zimmer, R.. Stabilizers for ergodic actions of higher rank semisimple groups. Ann. of Math. (2) 139(3) (1994), 723–747.CrossRefGoogle Scholar
Tucker-Drob, R.. Mixing actions of countable groups are almost free. Preprint, 2012, arXiv:1208.0655.Google Scholar
Tucker-Drob, R.. Shift-minimal groups, fixed price 1, and the unique trace property. Preprint, 2012,arXiv:1211.6395.Google Scholar
Vershik, A. M.. Nonfree actions of countable groups and their characters. J. Math. Sci. 174(1) (2011), 1–6.CrossRefGoogle Scholar
Vershik, A. M.. Totally nonfree actions and the infinite symmetric group. Mosc. Math. J. 12 (2012), 193–212.CrossRefGoogle Scholar
Zimmer, R.. Hyperfinite factors and amenable group actions. Invent. Math. 41(1) (1977), 23–31.CrossRefGoogle Scholar
Zimmer, R.. Ergodic theory, semi-simple lie groups, and foliations by manifolds of negative curvature. Publ. Math. Inst. Hautes Études Sci. 55(1) (1982), 37–62.CrossRefGoogle Scholar
Zimmer, R.. Ergodic Theory and Semisimple Groups. Birkhauser, Basel, 1984.CrossRefGoogle Scholar