Hostname: page-component-f554764f5-nwwvg Total loading time: 0 Render date: 2025-04-14T19:01:42.620Z Has data issue: false hasContentIssue false
  • English
  • Français

Spherical normal forms for germs of parabolic line biholomorphisms

Part of: Complex dynamical systems Differential equations in the complex domain

Published online by Cambridge University Press:  07 April 2025

LOÏC TEYSSIER
LOÏC TEYSSIER*
Affiliation:
Laboratoire IRMA (UMR 7501), Université de Strasbourg—CNRS, Strasbourg, France
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We address the inverse problem for holomorphic germs of a mapping of the complex line near a fixed point which is tangent to the identity. We provide a preferred parabolic map $\Delta $ realizing a given Birkhoff–Écalle–Voronin modulus 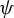$\psi $ and prove its uniqueness in the functional class we introduce. The germ is the time-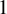$1$ map of a Gevrey formal vector field admitting meromorphic sums on a pair of infinite sectors covering the Riemann sphere. For that reason, the analytic continuation of $\Delta $ is a multivalued map admitting finitely many branch points with finite monodromy. In particular, $\Delta $ is holomorphic and injective on an open slit sphere containing $0$ (the initial fixed point) and $\infty $, where the companion parabolic point is situated under the involution 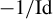${-1}/{\mathrm {Id}}$. One finds that the Birkhoff–Écalle–Voronin modulus of the parabolic germ at 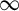$\infty $ is the inverse $\psi ^{\circ -1}$ of that at $0$.

Keywords

parabolic fixed-pointnormal formsinverse problemparabolic renormalization

MSC classification

Primary: 37F45: Holomorphic families of dynamical systems; the Mandelbrot set; bifurcations 37F75: Holomorphic foliations and vector fields
Secondary: 34M35: Singularities, monodromy, local behavior of solutions, normal forms 34M50: Inverse problems (Riemann-Hilbert, inverse differential Galois, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , First View , pp. 1 - 50
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Avila, A. and Lyubich, M.. Lebesgue measure of Feigenbaum Julia sets. Ann. of Math. (2) 195(1) (2022), 1–88.CrossRefGoogle Scholar
Baker, I. N.. Permutable entire functions. Math. Z. 79 (1962), 243–249.CrossRefGoogle Scholar
Buff, X. and Chéritat, A.. Quadratic Julia sets with positive area. Proceedings of the International Congress of Mathematicians. Volume III. Hindustan Book Agency, New Delhi, 2010, pp. 1701–1713.Google Scholar
Branner, B. and Dias, K.. Classification of complex polynomial vector fields in one complex variable. J. Difference Equ. Appl. 16(5–6) (2010), 463–517.CrossRefGoogle Scholar
Birkhoff, G. D.. Déformations analytiques et fonctions auto-équivalentes. Ann. Inst. H. Poincaré Anal. Non Linéaire 9 (1939), 51–122.Google Scholar
Douady, A., Estrada, F. and Sentenac, P.. Champs de vecteurs polynomiaux sur $\mathbb{C}$ . Preprint, 2005.Google Scholar
Écalle, J.. Théorie itérative: introduction à la théorie des invariants holomorphes. J. Math. Pures Appl. (9) 54 (1975), 183–258.Google Scholar
Écalle, J.. Les fonctions résurgentes. Tome III: l’équation du pont et la classification analytique des objects locaux. [The Bridge Equation and Analytic Classification of Local Objects] (Publications Mathématiques d’Orsay [Mathematical Publications of Orsay], 85). Université de Paris-Sud, Département de Mathématiques, Orsay, 1985.Google Scholar
Ecalle, J.. Twisted resurgence monomials and canonical-spherical synthesis of local objects. Analyzable Functions and Applications (Contemporary Mathematics, 373). American Mathematical Society, Providence, RI, 2005, pp. 207–315.CrossRefGoogle Scholar
Epstein, A.. Towers of finite type complex analytic maps. PhD Thesis, 1993.Google Scholar
Loray, F.. Versal deformation of the analytic saddle-node. Astérisque 297 (2004), 167–187; analyse complexe, systémes dynamiques, sommabilité des séries divergentes et théories galoisiennes. II.Google Scholar
Loday-Richaud, M.. Divergent Series, Summability and Resurgence. II. Simple and Multiple Summability (Lecture Notes in Mathematics, 2154). Springer, Cham, 2016; with prefaces by J.-P. Ramis, É. Delabaere, C. Mitschi and D. Sauzin.CrossRefGoogle Scholar
Rousseau, C. and Teyssier, L.. Analytic normal forms and inverse problems for unfoldings of 2-dimensional saddle-nodes with analytic center manifold. Ann. Sci. Éc. Norm. Supér. (4) 54(1) (2021), 133–233.CrossRefGoogle Scholar
Shishikura, M.. The Hausdorff dimension of the boundary of the Mandelbrot set and Julia sets. Ann. of Math. (2) 147(2) (1998), 225–267.CrossRefGoogle Scholar
Smale, S.. The fundamental theorem of algebra and complexity theory. Bull. Amer. Math. Soc. (N.S.) 4(1) (1981), 1–36.CrossRefGoogle Scholar
Schäfke, R. and Teyssier, L.. Analytic normal forms for convergent saddle-node vector fields. Ann. Inst. Fourier (Grenoble) 65(3) (2015), 933–974.CrossRefGoogle Scholar
Shub, M., Tischler, D. and Williams, R. F.. The Newtonian graph of a complex polynomial. SIAM J. Math. Anal. 19(1) (1988), 246–256.CrossRefGoogle Scholar
Voronin, S.. Analytic classification of germs of conformal mappings (C,0) → (C,0). Funct. Anal. Appl. 15(1) (1981), 1–13.CrossRefGoogle Scholar