Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-26T12:27:09.178Z Has data issue: false hasContentIssue false
  • English
  • Français

Skinning measures in negative curvature and equidistribution of equidistant submanifolds

Published online by Cambridge University Press:  30 April 2013

JOUNI PARKKONEN  and
FRÉDÉRIC PAULIN
JOUNI PARKKONEN
Affiliation:
Department of Mathematics and Statistics, PO Box 35, 40014 University of Jyväskylä, Finland email [email protected]
FRÉDÉRIC PAULIN
Affiliation:
Département de mathématique, UMR 8628 CNRS, Bât. 425, Université Paris-Sud, 91405 Orsay Cedex, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 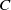$C$ be a locally convex closed subset of a negatively curved Riemannian manifold 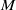$M$. We define the skinning measure 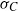${\sigma }_{C} $ on the outer unit normal bundle to 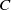$C$ in 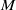$M$ by pulling back the Patterson–Sullivan measures at infinity, and give a finiteness result for 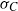${\sigma }_{C} $, generalizing the work of Oh and Shah, with different methods. We prove that the skinning measures, when finite, of the equidistant hypersurfaces to 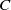$C$ equidistribute to the Bowen–Margulis measure 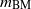${m}_{\mathrm{BM} } $ on 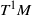${T}^{1} M$, assuming only that ${m}_{\mathrm{BM} } $ is finite and mixing for the geodesic flow. Under additional assumptions on the rate of mixing, we give a control on the rate of equidistribution.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 4 , August 2014 , pp. 1310 - 1342
Copyright
Copyright ©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Babillot, M.. On the mixing property for hyperbolic systems. Israel J. Math. 129 (2002), 61–76.Google Scholar
Bowditch, B.. Geometrical finiteness with variable negative curvature. Duke Math. J. 77 (1995), 229–274.Google Scholar
Bowen, R.. Periodic orbits for hyperbolic flows. Amer. J. Math. 94 (1972), 1–30.CrossRefGoogle Scholar
Bridson, M. R. and Haefliger, A.. Metric Spaces of Non-positive Curvature (Grundlehren der Mathematischen Wissenschaften, 319). Springer, 1999.Google Scholar
Brin, M.. Ergodicity of the geodesic flow. Appendix in W. Ballmann. Lectures on Spaces of Nonpositive Curvature (DMV Seminar, 25). Birkhäuser, 1995, pp. 81–95.Google Scholar
Clozel, L.. Démonstration de la conjecture $\tau $. Invent. Math. 151 (2003), 297–328.Google Scholar
Dal’Bo, F.. Remarques sur le spectre des longueurs d’une surface et comptage. Bol. Soc. Bras. Mat. 30 (1999), 199–221.CrossRefGoogle Scholar
Dal’Bo, F.. Topologie du feuilletage fortement stable. Ann. Inst. Fourier 50 (2000), 981–993.Google Scholar
Dal’Bo, F., Otal, J.-P. and Peigné, M.. Séries de Poincaré des groupes géométriquement finis. Israel J. Math. 118 (2000), 109–124.Google Scholar
Dolgopyat, D.. On decay of correlation in Anosov flows. Ann. of Math. (2) 147 (1998), 357–390.Google Scholar
Eskin, A. and McMullen, C.. Mixing, counting, and equidistribution in Lie groups. Duke Math. J. 71 (1993), 181–209.CrossRefGoogle Scholar
Giulietti, P., Liverani, C. and Pollicott, M.. Anosov flows and dynamical zeta functions. Ann. of Math. (2) to appear. Preprint, 2012, arXiv:1203.0904.Google Scholar
Hamenstädt, U.. A new description of the Bowen–Margulis measure. Ergod. Th. & Dynam. Sys. 9 (1989), 455–464.Google Scholar
Hersonsky, S. and Paulin, F.. On the rigidity of discrete isometry groups of negatively curved spaces. Comment. Math. Helv. 72 (1997), 349–388.Google Scholar
Hersonsky, S. and Paulin, F.. Counting orbit points in coverings of negatively curved manifolds and Hausdorff dimension of cusp excursions. Ergod. Th. & Dynam. Sys. 24 (2004), 1–22.Google Scholar
Hersonsky, S. and Paulin, F.. On the almost sure spiraling of geodesics in negatively curved manifolds. J. Differential Geom. 85 (2010), 271–314.Google Scholar
Kim, I.. Counting, mixing and equidistribution of horospheres in geometrically finite rank one locally symmetric manifolds. Preprint, 2011, arXiv:1103.5003.Google Scholar
Kinnunen, J., Korte, R., Shanmugalingam, N. and Tuominen, H.. A characterization of Newtonian functions with zero boundary values. Calc. Var. Partial Differential Equations 43 (2012), 507–528.Google Scholar
Kleinbock, D. and Margulis, G.. Bounded orbits of nonquasiunipotent flows on homogeneous spaces. Sinai’s Moscow Seminar on Dynamical Systems (American Mathematical Society Translations, Series 2, 171). American Mathematical Society, Providence, RI, 1996, pp. 141–172.Google Scholar
Kleinbock, D. and Margulis, G.. Logarithm laws for flows on homogeneous spaces. Invent. Math. 138 (1999), 451–494.Google Scholar
Kontorovich, A. and Oh, H.. Apollonian circle packings and closed horospheres on hyperbolic 3-manifolds. J. Amer. Math. Soc. 24 (2011), 603–648.CrossRefGoogle Scholar
Liverani, C.. On contact Anosov flows. Ann. of Math. (2) 159 (2004), 1275–1312.Google Scholar
Margulis, G.. Applications of ergodic theory for the investigation of manifolds of negative curvature. Funct. Anal. Appl. 3 (1969), 335–336.CrossRefGoogle Scholar
Margulis, G.. Certain measures that are connected with $U$-flows on compact manifolds. Funct. Anal. Appl. 4 (1970), 55–67.Google Scholar
Margulis, G.. On Some Aspects of the Theory of Anosov Systems (Monographs in Mathematics). Springer, 2004.Google Scholar
Marklof, J.. The asymptotic distribution of Frobenius numbers. Invent. Math. 181 (2010), 179–207.Google Scholar
Oh, H. and Shah, N.. The asymptotic distribution of circles in the orbits of Kleinian groups. Invent. Math. 187 (2012), 1–35.Google Scholar
Oh, H. and Shah, N.. Equidistribution and counting for orbits of geometrically finite hyperbolic groups. J. Amer. Math. Soc. 26 (2013), 511–562.Google Scholar
Otal, J.-P. and Peigné, M.. Principe variationnel et groupes kleiniens. Duke Math. J. 125 (2004), 15–44.Google Scholar
Parkkonen, J. and Paulin, F.. Équidistribution, comptage et approximation par irrationnels quadratiques. J. Mod. Dyn. 6 (2012), 1–40.Google Scholar
Parkkonen, J. and Paulin, F.. Counting arcs in negative curvature. Proc. Conf. Geometry, Topology, and Dynamics in Negative Curvature (Bangalore, 2010) (London Mathematical Society Lecture Notes), to appear. Preprint, 2012, arXiv:1203.0175.Google Scholar
Parkkonen, J. and Paulin, F.. Counting common perpendicular arcs in negative curvature, in preparation.Google Scholar
Paulin, F.. Regards croisés sur les séries de Poincaré et leurs applications. Notes d’exposé, GDR Platon 3341 CNRS, University of Neuchâtel, 7–9 February 2011, Monogr. Enseign. Math. to appear, see http://www.math.u-psud.fr/~paulin/preprints/liste_preprints.html.Google Scholar
Paulin, F., Pollicott, M. and Schapira, B.. Equilibrium states in negative curvature. Preprint, 2012, arXiv:1211.6242.Google Scholar
Roblin, T.. Sur la fonction orbitale des groupes discrets en courbure négative. Ann. Inst. Fourier 52 (2002), 145–151.Google Scholar
Roblin, T.. Ergodicité et équidistribution en courbure négative (Mémoires de la Société Mathématique de France, 95). Société Mathématique de France, Paris, 2003.Google Scholar
Schapira, B.. Lemme de l’ombre et non divergence des horosphères d’une variété géométriquement finie. Ann. Inst. Fourier (Grenoble) 54 (2004), 939–987.Google Scholar
Semmes, S.. Finding curves on general spaces through quantitative topology, with applications to Sobolev and Poincaré inequalities. Selecta Math. 2 (1996), 155–295.Google Scholar
Stoyanov, L.. Spectra of Ruelle transfer operators for axiom A flows. Nonlinearity 24 (2011), 1089–1120.Google Scholar
Stratmann, B. and Velani, S. L.. The Patterson measure for geometrically finite groups with parabolic elements, new and old. Proc. Lond. Math. Soc. 71 (1995), 197–220.Google Scholar
Sullivan, D.. Entropy, Hausdorff measures old and new, and the limit set of geometrically finite Kleinian groups. Acta Math. 153 (1984), 259–277.Google Scholar
Walter, R.. Some analytical properties of geodesically convex sets. Abh. Math. Semin. Univ. Hambg. 45 (1976), 263–282.Google Scholar
Ziemer, W. P.. Weakly Differentiable Functions (Graduate Texts in Mathematics, 120). Springer, 1989.Google Scholar