Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T01:15:50.145Z Has data issue: false hasContentIssue false
  • English
  • Français

Simultaneous dense and non-dense orbits for toral diffeomorphisms

Published online by Cambridge University Press:  28 January 2016

JIMMY TSENG
JIMMY TSENG*
Affiliation:
School of Mathematics, University of Bristol, University Walk, Bristol BS8 1TW, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that, for pairs of hyperbolic toral automorphisms on the $2$-torus, the points with dense forward orbits under one map and non-dense forward orbits under the other is a dense, uncountable set. The pair of maps can be non-commuting. We also show the same for pairs of 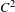$C^{2}$-Anosov diffeomorphisms on the $2$-torus. (The pairs must satisfy slight constraints.) Our main tools are the Baire category theorem and a geometric construction that allows us to give a geometric characterization of the fractal that is the set of points with forward orbits that miss a certain open set.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 4 , June 2017 , pp. 1308 - 1322
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bergelson, V., Einsiedler, M. and Tseng, J.. Simultaneous dense and nondense orbits for commuting maps. Israel J. Math. Preprint, 2013, arXiv:1309.4823.Google Scholar
Broderick, R., Fishman, L. and Kleinbock, D.. Schmidt’s game, fractals, and orbits of toral endomorphisms. Ergod. Th. & Dynam. Sys. 31 (2011), 1095–1107.CrossRefGoogle Scholar
Hirsch, M. W. and Pugh, C. C.. Stable manifolds and hyperbolic sets. Global Analysis (Proc. Sympos. Pure Math., Vol. XIV, Berkeley, CA, 1968). American Mathematical Society, Providence, RI, 1970, pp. 133–163.Google Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems. With a Supplementary Chapter by Katok and Leonardo Mendoza (Encyclopedia of Mathematics and its Applications, 54) . Cambridge University Press, Cambridge, 1995.Google Scholar
Lytle, B. and Maier, A.. Simultaneous dense and nondense points for noncommuting toral endomorphisms. Preprint, 2014, arXiv:1407.4014.Google Scholar
Shi, R. and Tseng, J.. Simultaneous dense and nondense orbits and the space of lattices. Int. Math. Res. Not. IMRN. Preprint, 2015, doi:10.1093/imrn/rnv018.Google Scholar
Tseng, J.. Schmidt games and Markov partitions. Nonlinearity 22 (2009), 525–543.Google Scholar
Tseng, J.. Nondense orbits for Anosov diffeomorphisms of the 2-torus. Preprint, 2015, arXiv:1503.02273.Google Scholar
Urbański, M.. The Hausdorff dimension of the set of points with nondense orbit under a hyperbolic dynamical system. Nonlinearity 4 (1991), 385–397.Google Scholar