Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bastos, Jéfferson L.R.
Caprio, Danilo A.
and
Messaoudi, Ali
2021.
Shadowing and stability in p-adic dynamics.
Journal of Mathematical Analysis and Applications,
Vol. 500,
Issue. 2,
p.
125117.
Bayart, Frédéric
2021.
Two problems on weighted shifts in linear dynamics.
Proceedings of the American Mathematical Society,
Vol. 149,
Issue. 12,
p.
5255.
Alves, Fabricio F.
Bernardes, Nilson C.
and
Messaoudi, Ali
2021.
Chain recurrence and average shadowing in dynamics.
Monatshefte für Mathematik,
Vol. 196,
Issue. 4,
p.
665.
D'Aniello, Emma
Darji, Udayan B.
and
Maiuriello, Martina
2021.
Generalized hyperbolicity and shadowing in L spaces.
Journal of Differential Equations,
Vol. 298,
Issue. ,
p.
68.
Lopes, Artur O
Messaoudi, Ali
Stadlbauer, Manuel
and
Vargas, Victor
2021.
Invariant probabilities for discrete time linear dynamics via thermodynamic formalism
*
.
Nonlinearity,
Vol. 34,
Issue. 12,
p.
8359.
Lopes, Artur O.
and
Vargas, Victor
2022.
Entropy, Pressure, Ground States and Calibrated Sub-actions for Linear Dynamics.
Bulletin of the Brazilian Mathematical Society, New Series,
Vol. 53,
Issue. 3,
p.
1073.
Backes, Lucas
and
Dragičević, Davor
2022.
A generalized Grobman–Hartman theorem for nonautonomous dynamics.
Collectanea Mathematica,
Vol. 73,
Issue. 3,
p.
411.
Lee, J
and
Rojas, A
2022.
A topological shadowing theorem.
Proceedings - Mathematical Sciences,
Vol. 132,
Issue. 1,
Bongiorno, D.
D’Aniello, E.
Darji, U.
and
Di Piazza, L.
2022.
Linear dynamics induced by odometers.
Proceedings of the American Mathematical Society,
Vol. 150,
Issue. 7,
p.
2823.
Maiuriello, Martina
2022.
Expansivity and strong structural stability for composition operators on $$L^p$$ spaces.
Banach Journal of Mathematical Analysis,
Vol. 16,
Issue. 4,
Lee, K.
and
Morales, C. A.
2022.
Hyperbolicity, Shadowing, and Bounded Orbits.
Qualitative Theory of Dynamical Systems,
Vol. 21,
Issue. 3,
Antunes, Mayara Braz
Mantovani, Gabriel Elias
and
Varão, Régis
2022.
Chain recurrence and positive shadowing in linear dynamics.
Journal of Mathematical Analysis and Applications,
Vol. 506,
Issue. 1,
p.
125622.
D'Aniello, Emma
Darji, Udayan B.
and
Maiuriello, Martina
2022.
Shift-like operators on L(X).
Journal of Mathematical Analysis and Applications,
Vol. 515,
Issue. 1,
p.
126393.
Lee, J.
and
Morales, C. A.
2023.
Hyperbolicity, shadowing, and convergent operators.
Monatshefte für Mathematik,
Vol. 202,
Issue. 3,
p.
541.
Morales, C. A.
and
Nguyen, T.
2023.
Quantifying the Shadowing Property.
Journal of Dynamics and Differential Equations,
Morales, C. A.
and
Linh, T. T.
2024.
Shadowing, hyperbolicity, and Aluthge transforms.
Periodica Mathematica Hungarica,
Vol. 89,
Issue. 2,
p.
379.
Bernardes, Nilson C.
and
Peris, Alfred
2024.
On shadowing and chain recurrence in linear dynamics.
Advances in Mathematics,
Vol. 441,
Issue. ,
p.
109539.
Estaremi, Yousef
and
Muhammad, Shah
2024.
Li–Yorke chaos for composition operators on Orlicz spaces.
Forum Mathematicum,
Vol. 0,
Issue. 0,
Lee, Keonhee
and
Morales Rojas, Carlos A.
2024.
Topological stability, L-shadowing and generalized hyperbolicity.
Tunisian Journal of Mathematics,
Vol. 6,
Issue. 3,
p.
549.
Al Ghafri, Mohammed Said
Estaremi, Yousef
and
Huang, Zhidong
2024.
Orlicz Spaces and Their Hyperbolic Composition Operators.
Mathematics,
Vol. 12,
Issue. 18,
p.
2809.
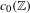 $c_{0}(\mathbb{Z})$ and
$c_{0}(\mathbb{Z})$ and 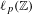 $\ell _{p}(\mathbb{Z})$ (
$\ell _{p}(\mathbb{Z})$ (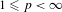 $1\leq p<\infty$) that satisfy the shadowing property.
$1\leq p<\infty$) that satisfy the shadowing property.


