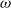Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-13T17:01:44.974Z Has data issue: false hasContentIssue false
  • English
  • Français

Shadowing and $\omega $-limit sets of circular Julia sets

Published online by Cambridge University Press:  14 November 2013

ANDREW D. BARWELL ,
JONATHAN MEDDAUGH  and
BRIAN E. RAINES
ANDREW D. BARWELL
Affiliation:
Heilbronn Institute of Mathematical Research, University of Bristol, Howard House, Queens Avenue, Bristol, BS8 1SN, UK email [email protected] School of Mathematics, University of Birmingham, Birmingham, B15 2TT, UK email [email protected]
JONATHAN MEDDAUGH
Affiliation:
Department of Mathematics, Baylor University, Waco, TX 76798–7328, USA email [email protected][email protected]
BRIAN E. RAINES
Affiliation:
Department of Mathematics, Baylor University, Waco, TX 76798–7328, USA email [email protected][email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we consider quadratic polynomials on the complex plane 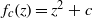${f}_{c} (z)= {z}^{2} + c$ and their associated Julia sets, 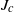${J}_{c} $. Specifically, we consider the case that the kneading sequence is periodic and not an $n$-tupling. In this case 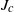${J}_{c} $ contains subsets that are homeomorphic to the unit circle, usually infinitely many disjoint such subsets. We prove that 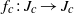${f}_{c} : {J}_{c} \rightarrow {J}_{c} $ has shadowing, and we classify all 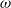$\omega $-limit sets for these maps by showing that a closed set 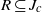$R\subseteq {J}_{c} $ is internally chain transitive if, and only if, there is some 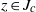$z\in {J}_{c} $ with $\omega (z)= R$.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 4 , June 2015 , pp. 1045 - 1055
Copyright
© Cambridge University Press, 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baldwin, S.. Continuous itinerary functions and dendrite maps. Topology Appl. 154 (16) (2007), 2889–2938.CrossRefGoogle Scholar
Baldwin, S.. Julia sets and periodic kneading sequences. J. Fixed Point Theory Appl. 7 (1) (2010), 201–222.CrossRefGoogle Scholar
Barwell, A., Good, C., Knight, R. and Raines, B. E.. A characterization of $\omega $-limit sets in shift spaces. Ergod. Th. & Dynam. Sys. 30 (1) (2010), 21–31.CrossRefGoogle Scholar
Barwell, A. D.. A characterization of $\omega $-limit sets of piecewise monotone maps of the interval. Fund. Math. 207 (2) (2010), 161–174.CrossRefGoogle Scholar
Barwell, A. D., Good, C., Oprocha, P. and Raines, B. E.. Characterizations of $\omega $-limit sets of topologically hyperbolic spaces. Discrete Contin. Dyn. Syst. 33 (5) (2013), 1819–1833.CrossRefGoogle Scholar
Barwell, A. D. and Raines, B.. The $\omega $-limit sets of quadratic Julia sets. Ergod. Th. & Dynam. Sys. (2013) to appear.CrossRefGoogle Scholar
Barwell, A. D., Davies, G. and Good, C.. On the $\omega $-limit sets of tent maps. Fund. Math. 217 (1) (2012), 35–54.CrossRefGoogle Scholar
Hirsch, M. W., Smith, H. L. and Zhao, X.-Q.. Chain transitivity, attractivity, and strong repellors for semidynamical systems. J. Dynam. Differential Equations 13 (1) (2001), 107–131.CrossRefGoogle Scholar
Keller, K.. Invariant Factors, Julia Equivalences and the (Abstract) Mandelbrot Set (Lecture Notes in Mathematics, 1732). Springer, Berlin, 2000.CrossRefGoogle Scholar
Moore, R. L.. Concerning essential continua of condensation. Trans. Amer. Math. Soc. 42 (1) (1937), 41–52.CrossRefGoogle Scholar
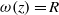Whyburn, G. T.. Analytic Topology. American Mathematical Society Colloquium Publications, New York, 1971.Google Scholar