Published online by Cambridge University Press: 04 November 2020
The papers [O. M. Sarig. Symbolic dynamics for surface diffeomorphisms with positive entropy. J. Amer. Math. Soc.26(2) (2013), 341–426] and [S. Ben Ovadia. Symbolic dynamics for non-uniformly hyperbolic diffeomorphisms of compact smooth manifolds. J. Mod. Dyn.13 (2018), 43–113] constructed symbolic dynamics for the restriction of
 $C^r$
diffeomorphisms to a set
$C^r$
diffeomorphisms to a set
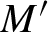 $M'$
with full measure for all sufficiently hyperbolic ergodic invariant probability measures, but the set
$M'$
with full measure for all sufficiently hyperbolic ergodic invariant probability measures, but the set
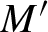 $M'$
was not identified there. We improve the construction in a way that enables
$M'$
was not identified there. We improve the construction in a way that enables
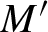 $M'$
to be identified explicitly. One application is the coding of infinite conservative measures on the homoclinic classes of Rodriguez-Hertz et al. [Uniqueness of SRB measures for transitive diffeomorphisms on surfaces. Comm. Math. Phys.306(1) (2011), 35–49].
$M'$
to be identified explicitly. One application is the coding of infinite conservative measures on the homoclinic classes of Rodriguez-Hertz et al. [Uniqueness of SRB measures for transitive diffeomorphisms on surfaces. Comm. Math. Phys.306(1) (2011), 35–49].