Hostname: page-component-669899f699-tzmfd Total loading time: 0 Render date: 2025-04-24T19:18:06.076Z Has data issue: false hasContentIssue false
  • English
  • Français

Sequence entropy tuples and mean sensitive tuples

Part of: Ergodic theory Topological dynamics

Published online by Cambridge University Press:  20 February 2023

JIE LI ,
CHUNLIN LIU Open the ORCID record for CHUNLIN LIU [Opens in a new window] ,
SIMING TU  and
TAO YU
JIE LI
Affiliation:
School of Mathematics and Statistics, Jiangsu Normal University, Xuzhou, Jiangsu 221116, P. R. China (e-mail: [email protected])
CHUNLIN LIU*
Affiliation:
CAS Wu Wen-Tsun Key Laboratory of Mathematics, School of Mathematical Sciences, University of Science and Technology of China, Hefei, Anhui 230026, P. R. China
SIMING TU
Affiliation:
School of Mathematics (Zhuhai), Sun Yat-sen University, Zhuhai, Guangdong 519082, P. R. China (e-mail: [email protected])
TAO YU
Affiliation:
Department of Mathematics, Shantou University, Shantou 515063, P. R. China (e-mail: [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Using the idea of local entropy theory, we characterize the sequence entropy tuple via mean forms of the sensitive tuple in both topological and measure-theoretical senses. For the measure-theoretical sense, we show that for an ergodic measure-preserving system, the 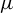$\mu $-sequence entropy tuple, the 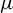$\mu $-mean sensitive tuple, and the 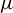$\mu $-sensitive in the mean tuple coincide, and give an example to show that the ergodicity condition is necessary. For the topological sense, we show that for a certain class of minimal systems, the mean sensitive tuple is the sequence entropy tuple.

Keywords

sequence entropy tuplesmean sensitive tuplessensitive in the mean tuples

MSC classification

Primary: 37A35: Entropy and other invariants, isomorphism, classification 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 44 , Issue 1 , January 2024 , pp. 184 - 203
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Blanchard, F.. Fully positive topological entropy and topological mixing. Symbolic dynamics and its applications. Contemp. Math. 135 (1992), 95–105.CrossRefGoogle Scholar
Blanchard, F.. A disjointness theorem involving topological entropy. Bull. Soc. Math. France 121 (1993), 465–478.CrossRefGoogle Scholar
Blanchard, F., Glasner, E. and Host, B.. A variation on the variational principle and applications to entropy pairs. Ergod. Th. & Dynam. Sys. 17 (1997), 29–43.CrossRefGoogle Scholar
Blanchard, F., Host, B., Maass, A., Martinez, S. and Rudolph, D.. Entropy pairs for a measure. Ergod. Th. & Dynam. Sys. 15 (1995), 621–632.CrossRefGoogle Scholar
Downarowicz, T. and Glasner, E.. Isomorphic extensions and applications. Topol. Methods Nonlinear Anal. 48(1) (2016), 321–338.Google Scholar
Fuhrmann, G., Glasner, E., Jäger, T. and Oertel, C.. Irregular model sets and tame dynamics. Trans. Amer. Math. Soc. 374 (2021), 3703–3734.CrossRefGoogle Scholar
García-Ramos, F.. Weak forms of topological and measure theoretical equicontinuity: relationships with discrete spectrum and sequence entropy. Ergod. Th. & Dynam. Sys. 37 (2017), 1211–1237.CrossRefGoogle Scholar
García-Ramos, F., Jäger, T. and Ye, X.. Mean equicontinuity, almost automorphy and regularity. Israel J. Math. 243 (2021), 155–183.CrossRefGoogle Scholar
García-Ramos, F. and Muñoz-López, V.. Measure-theoretic sequence entropy pairs and mean sensivity. Preprint, 2022, arXiv2210.15004.CrossRefGoogle Scholar
Glasner, E. and Ye, X.. Local entropy theory. Ergod. Th. & Dynam. Sys. 29 (2009), 321–356.CrossRefGoogle Scholar
Huang, W.. Tame systems and scrambled pairs under an abelian group action. Ergod. Th. & Dynam. Sys. 26(5) (2006), 1549–1567.CrossRefGoogle Scholar
Huang, W., Li, S., Shao, S. and Ye, X.. Null systems and sequence entropy pairs. Ergod. Th. & Dynam. Sys. 23(5) (2003), 1505–1523.CrossRefGoogle Scholar
Huang, W., Lian, Z., Shao, S. and Ye, X.. Minimal systems with finitely many ergodic measures. J. Funct. Anal. 280 (2021), 109000.CrossRefGoogle Scholar
Huang, W., Lu, P. and Ye, X.. Measure-theoretical sensitivity and equicontinuity. Israel J. Math. 183 (2011), 233–283.CrossRefGoogle Scholar
Huang, W., Maass, A. and Ye, X.. Sequence entropy pairs and complexity pairs for a measure. Ann. Inst. Fourier (Grenoble) 54 (2004), 1005–1028.CrossRefGoogle Scholar
Huang, W. and Ye, X.. A local variational relation and applications. Israel J. Math. 151 (2006), 237–279.CrossRefGoogle Scholar
Huang, W. and Ye, X.. Combinatorial lemmas and applications to dynamics. Adv. Math. 220 (2009), 1689–1716.CrossRefGoogle Scholar
Kerr, D. and Li, H.. Independence in topological and C*-dynamics. Math. Ann. 338 (2007), 869–926.CrossRefGoogle Scholar
Kerr, D. and Li, H.. Combinatorial independence in measurable dynamics. J. Funct. Anal. 256 (2009), 1341–1386.CrossRefGoogle Scholar
Kra, B., Moreira, J., Richter, F. and Robertson, D.. Infinite sumsets in sets with positive density. Preprint, 2022, arXiv:2206.0178.CrossRefGoogle Scholar
Kra, B., Moreira, J., Richter, F. and Robertson, D.. A proof of Erdös’s B+B+t conjecture. Preprint, 2022, arXiv:2206.12377.Google Scholar
Kušhnirenko, A. G.. Metric invariants of entropy type. Uspekhi Mat. Nauk 22(137(5)) (1967), 57–65 (in Russian).Google Scholar
Li, J.. Measure-theoretic sensitivity via finite partitions. Nonlinearity 29 (2016), 2133–2144.CrossRefGoogle Scholar
Li, J. and Tu, S.. Density-equicontinuity and density-sensitivity. Acta Math. Sin. (Engl. Ser.) 37(2) (2021), 345–361.CrossRefGoogle Scholar
Li, J., Tu, S. and Ye, X.. Mean equicontinuity and mean sensitivity. Ergod. Th. & Dynam. Sys. 35 (2015), 2587–2612.CrossRefGoogle Scholar
Li, J., Ye, X. and Yu, T.. Mean equicontinuity, complexity and applications. Discrete Contin. Dyn. Syst. 41(1) (2021), 359–393.CrossRefGoogle Scholar
Li, J., Ye, X. and Yu, T.. Equicontinuity and sensitivity in mean forms. J. Dynam. Differential Equations 34 (2022), 133–154.CrossRefGoogle Scholar
Li, J. and Yu, T.. On mean sensitive tuples. J. Differential Equations 297 (2021), 175–200.CrossRefGoogle Scholar
Maass, A. and Shao, S.. Structure of bounded topological-sequence-entropy minimal systems. J. Lond. Math. Soc. 76 (2007), 702–718.CrossRefGoogle Scholar
Ruelle, D.. Dynamical systems with turbulent behavior. Mathematical Problems in Theoretical Physics (Proc. Int. Conf., Rome, June 6–15, 1977) (Lecture Notes in Physics, 80). Eds. Dell'Antonio, G., Doplicher, S. and Jona-Lasinio, G.. Springer, Berlin, 1978, pp. 341–360.Google Scholar
Xiong, J.. Chaos in a topologically transitive system. Sci. China Ser. A 48 (2005), 929–939.CrossRefGoogle Scholar
Ye, X. and Zhang, R.. On sensitive sets in topological dynamics. Nonlinearity 21 (2008), 1601–1620.CrossRefGoogle Scholar
Yu, T.. Measure-theoretic mean equicontinuity and bounded complexity. J. Differential Equations 267 (2019), 6152–6170.CrossRefGoogle Scholar