Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-27T11:32:15.819Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-embeddings of Bedford–McMullen carpets

Published online by Cambridge University Press:  17 August 2017

AMIR ALGOM  and
MICHAEL HOCHMAN
AMIR ALGOM
Affiliation:
Einstein Institute of Mathematics, Edmond J. Safra Campus, The Hebrew University of Jerusalem, Givat Ram, Jerusalem, 9190401, Israel email [email protected], [email protected]
MICHAEL HOCHMAN
Affiliation:
Einstein Institute of Mathematics, Edmond J. Safra Campus, The Hebrew University of Jerusalem, Givat Ram, Jerusalem, 9190401, Israel email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 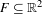$F\subseteq \mathbb{R}^{2}$ be a Bedford–McMullen carpet defined by multiplicatively independent exponents, and suppose that either $F$ is not a product set, or it is a product set with marginals of dimension strictly between zero and one. We prove that any similarity $g$ such that 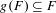$g(F)\subseteq F$ is an isometry composed of reflections about lines parallel to the axes. Our approach utilizes the structure of tangent sets of $F$, obtained by ‘zooming in’ on points of $F$, projection theorems for products of self-similar sets, and logarithmic commensurability type results for self-similar sets in the line.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 3 , March 2019 , pp. 577 - 603
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bandt, C. and Käenmäki, A.. Local structure of self-affine sets. Ergod. Th. & Dynam. Sys. 33(05) (2013), 1326–1337.Google Scholar
Bishop, C. J. and Peres, Y.. Fractals in Probability and Analysis (Cambridge Studies in Advanced Mathematics, 162) . Cambridge University Press, Cambridge, UK, 2016.Google Scholar
Elekes, M., Keleti, T. and Máthé, A.. Self-similar and self-affine sets: measure of the intersection of two copies. Ergod. Th. & Dynam. Sys. 30(2) (2010), 399–440.Google Scholar
Feng, D.-J., Huang, W. and Rao, H.. Affine embeddings and intersections of Cantor sets. J. Math. Pures Appl. (9) 102(6) (2014), 1062–1079.Google Scholar
Feng, D.-J. and Wang, Y.. On the structures of generating iterated function systems of Cantor sets. Adv. Math. 222(6) (2009), 1964–1981.Google Scholar
Furstenberg, H.. Disjointness in ergodic theory, minimal sets, and a problem in diophantine approximation. Math. Systems Theory 1(1) (1967), 1–49.Google Scholar
Hochman, M.. Geometric rigidity of × m invariant measures. J. Eur. Math. Soc. (JEMS) 14(5) (2012), 1539–1563.Google Scholar
Hochman, M. and Shmerkin, P.. Local entropy averages and projections of fractal measures. Ann. of Math. (2) 175(3) (2012), 1001–1059.Google Scholar
Hochman, M. and Shmerkin, P.. Equidistribution from fractal measures. Invent. Math. 202(1) (2015), 427–479.Google Scholar
Hutchinson, J. E.. Fractals and Self Similarity. Department of Mathematics, University of Melbourne, 1979.Google Scholar
Käenmäki, A., Koivusalo, H. and Rossi, E.. Self-affine sets with fibered tangents. Ergod. Th. & Dynam. Sys. doi:10.1017/etds.2015.130. Published online 28 January 2016.Google Scholar
Käenmäki, A., Ojala, T. and Rossi, E.. Rigidity of quasisymmetric mappings on self-affine carpets. Int. Math. Res. Not. (2016), to appear.Google Scholar
Peres, Y.. The self-affine carpets of McMullen and Bedford have infinite Hausdorff measure. Math. Proc. Cambridge Philos. Soc. 116(11) (1994), 513–526.Google Scholar
Peres, Y. and Shmerkin, P.. Resonance between Cantor sets. Ergod. Th. & Dynam. Sys. 29(1) (2009), 201–221.Google Scholar