Article contents
Sarnak’s conjecture for sequences of almost quadratic word growth
Published online by Cambridge University Press: 04 December 2020
Abstract
We prove the logarithmic Sarnak conjecture for sequences of subquadratic word growth. In particular, we show that the Liouville function has at least quadratically many sign patterns. We deduce the main theorem from a variant which bounds the correlations between multiplicative functions and sequences with subquadratically many words which occur with positive logarithmic density. This allows us to actually prove that our multiplicative functions do not locally correlate with sequences of subquadratic word growth. We also prove a conditional result which shows that if the (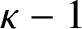 $\kappa -1$
)-Fourier uniformity conjecture holds then the Liouville function does not correlate with sequences with
$\kappa -1$
)-Fourier uniformity conjecture holds then the Liouville function does not correlate with sequences with
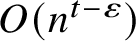 $O(n^{t-\varepsilon })$
many words of length n where
$O(n^{t-\varepsilon })$
many words of length n where
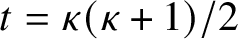 $t = \kappa (\kappa +1)/2$
. We prove a variant of the
$t = \kappa (\kappa +1)/2$
. We prove a variant of the
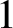 $1$
-Fourier uniformity conjecture where the frequencies are restricted to any set of box dimension less than
$1$
-Fourier uniformity conjecture where the frequencies are restricted to any set of box dimension less than
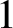 $1$
.
$1$
.
MSC classification
- Type
- Original Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike licence (http://creativecommons.org/licenses/by-nc-sa/4.0/), which permits non-commercial re-use, distribution, and reproduction in any medium, provided the same Creative Commons licence is included and the original work is properly cited. The written permission of Cambridge University Press must be obtained for commercial re-use.
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
REFERENCES
- 3
- Cited by



