Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mackay, R.S.
and
Tresser, C.
1986.
Transition to topological chaos for circle maps.
Physica D: Nonlinear Phenomena,
Vol. 19,
Issue. 2,
p.
206.
Misiurewicz, Michał
1986.
Rotation intervals for a class of maps of the real line into itself.
Ergodic Theory and Dynamical Systems,
Vol. 6,
Issue. 1,
p.
117.
Barkmeijer, Jan
1988.
The speed interval: a rotation algorithm for endomorphisms of the circle.
Ergodic Theory and Dynamical Systems,
Vol. 8,
Issue. 1,
p.
17.
Barge, Marcy
and
Swanson, Richard
1988.
Rotation shadowing properties of circle and annulus maps.
Ergodic Theory and Dynamical Systems,
Vol. 8,
Issue. 4,
p.
509.
Dufour, Jean-Paul
1989.
Existence de cycles pour des multi-applications du cercle.
Ergodic Theory and Dynamical Systems,
Vol. 9,
Issue. 1,
p.
47.
Zheng, Wei-Mou
1989.
The W sequence for circle maps and misbehaved itineraries.
Journal of Physics A: Mathematical and General,
Vol. 22,
Issue. 17,
p.
3647.
Blokh, A. M.
1990.
On dynamical systems on one-dimensional branched manifolds. III.
Journal of Soviet Mathematics,
Vol. 49,
Issue. 2,
p.
875.
Llibre, J.
and
Mackay, R. S.
1991.
Rotation vectors and entropy for homeomorphisms of the torus isotopic to the identity.
Ergodic Theory and Dynamical Systems,
Vol. 11,
Issue. 1,
p.
115.
Krupa, Martin
and
Roberts, Mark
1992.
Symmetry breaking and symmetry locking in equivariant circle maps.
Physica D: Nonlinear Phenomena,
Vol. 57,
Issue. 3-4,
p.
417.
Esquembre, Francisco
1993.
Twist orbits for non continuous maps of degree one.
Bulletin of the Australian Mathematical Society,
Vol. 47,
Issue. 3,
p.
415.
SAUM, MICHAEL A.
and
YOUNG, TODD R.
2001.
OBSERVED ROTATION NUMBERS IN FAMILIES OF CIRCLE MAPS.
International Journal of Bifurcation and Chaos,
Vol. 11,
Issue. 01,
p.
73.
ALSEDÀ, LLUÍS
MAÑOSAS, FRANCESC
and
CHAS, MOIRA
2002.
ROTATION SETS FOR ORBITS OF DEGREE ONE CIRCLE MAPS.
International Journal of Bifurcation and Chaos,
Vol. 12,
Issue. 02,
p.
429.
Hunt, Brian
and
Young, Todd
2004.
Critical saddle-node bifurcations and Morse–Smale maps.
Physica D: Nonlinear Phenomena,
Vol. 197,
Issue. 1-2,
p.
1.
Tsai, Tsung-Lung
and
Dawes, Jonathan H.P.
2013.
Dynamics near a periodically-perturbed robust heteroclinic cycle.
Physica D: Nonlinear Phenomena,
Vol. 262,
Issue. ,
p.
14.
Afraimovich, Valentin
Courbage, Maurice
and
Glebsky, Lev
2015.
Directional complexity and entropy for lift mappings.
Discrete & Continuous Dynamical Systems - B,
Vol. 20,
Issue. 10,
p.
3385.
Andres, Jan
2020.
Coexistence of Subharmonic Periodic Solutions Having Various Periods of Differential Inclusions on the Circle with Admissible Impulses of Degrees $$D=-1,0,1$$.
Journal of Dynamics and Differential Equations,
Vol. 32,
Issue. 4,
p.
1731.
Efremova, L. S.
and
Makhrova, E. N.
2021.
One-dimensional dynamical systems.
Russian Mathematical Surveys,
Vol. 76,
Issue. 5,
p.
821.
Efremova, Lyudmila Sergeevna
and
Makhrova, Elena Nikolaevna
2021.
Одномерные динамические системы.
Успехи математических наук,
Vol. 76,
Issue. 5(461),
p.
81.
Jiang, Weifeng
2024.
Generalized rotation sets and rotational entropy for circle maps.
Journal of Mathematical Analysis and Applications,
Vol. 534,
Issue. 2,
p.
128090.


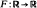 is defined as
is defined as 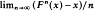 . We investigate the case where
. We investigate the case where 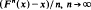 , as a function of
, as a function of 