Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
GRIESMER, JOHN T.
2019.
Recurrence, rigidity, and popular differences.
Ergodic Theory and Dynamical Systems,
Vol. 39,
Issue. 5,
p.
1299.
Cuny, Christophe
Eisner, Tanja
and
Farkas, Bálint
2019.
Wiener's lemma along primes and other subsequences.
Advances in Mathematics,
Vol. 347,
Issue. ,
p.
340.
Kanigowski, Adam
and
Lemańczyk, Mariusz
2020.
Encyclopedia of Complexity and Systems Science.
p.
1.
Badea, Catalin
Grivaux, Sophie
and
Matheron, Étienne
2021.
Rigidity sequences, Kazhdan sets and group topologies on the integers.
Journal d'Analyse Mathématique,
Vol. 143,
Issue. 1,
p.
313.
Haddock, Beatrix
Leng, James
and
Silva, Cesar E.
2022.
Nonsingular transformations that are ergodic with isometric coefficients and not weakly doubly ergodic.
Indagationes Mathematicae,
Vol. 33,
Issue. 6,
p.
1297.
Ackelsberg, Ethan M.
2022.
Rigidity, weak mixing, and recurrence in abelian groups.
Discrete & Continuous Dynamical Systems,
Vol. 42,
Issue. 4,
p.
1669.
Adams, Terrence
and
Quas, Anthony
2022.
Encyclopedia of Complexity and Systems Science.
p.
1.
Kanigowski, Adam
Kułaga-Przymus, Joanna
Lemańczyk, Mariusz
and
de la Rue, Thierry
2023.
On arithmetic functions orthogonal to deterministic sequences.
Advances in Mathematics,
Vol. 428,
Issue. ,
p.
109138.
Adams, Terrence
and
Quas, Anthony
2023.
Ergodic Theory.
p.
35.
Kanigowski, Adam
and
Lemańczyk, Mariusz
2023.
Ergodic Theory.
p.
109.
DONOSO, SEBASTIÁN
MAASS, ALEJANDRO
and
RADIĆ, TRISTÁN
2025.
On partial rigidity of
$\mathcal {S}$
-adic subshifts.
Ergodic Theory and Dynamical Systems,
p.
1.
Griesmer, John T.
2025.
Separating measurable recurrence from strong recurrence via rigidity sequences.
Discrete and Continuous Dynamical Systems,
Vol. 45,
Issue. 9,
p.
3411.
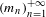 $(m_{n})_{n=1}^{+\infty }$ with the property that
$(m_{n})_{n=1}^{+\infty }$ with the property that 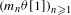 $(m_{n}{\it\theta}[1])_{n\geq 1}$ is dense in
$(m_{n}{\it\theta}[1])_{n\geq 1}$ is dense in  $\mathbb{T}$ for any
$\mathbb{T}$ for any 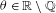 ${\it\theta}\in \mathbb{R}\setminus \mathbb{Q}$, and a continuous measure on the circle
${\it\theta}\in \mathbb{R}\setminus \mathbb{Q}$, and a continuous measure on the circle 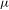 ${\it\mu}$ such that
${\it\mu}$ such that 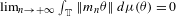 $\lim _{n\rightarrow +\infty }\int _{\mathbb{T}}\Vert m_{n}{\it\theta}\Vert \,d{\it\mu}({\it\theta})=0$. Moreover, for every fixed
$\lim _{n\rightarrow +\infty }\int _{\mathbb{T}}\Vert m_{n}{\it\theta}\Vert \,d{\it\mu}({\it\theta})=0$. Moreover, for every fixed 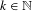 $k\in \mathbb{N}$, the set
$k\in \mathbb{N}$, the set 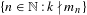 $\{n\in \mathbb{N}:k\nmid m_{n}\}$ is infinite. This is a sufficient condition for the existence of a rigid, weakly mixing dynamical system whose rigidity time is not a rigidity time for any system with a discrete part in its spectrum.
$\{n\in \mathbb{N}:k\nmid m_{n}\}$ is infinite. This is a sufficient condition for the existence of a rigid, weakly mixing dynamical system whose rigidity time is not a rigidity time for any system with a discrete part in its spectrum.