Published online by Cambridge University Press: 17 March 2023
Let G be a countably infinite discrete amenable group. It should be noted that a G-system 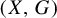 $(X,G)$ naturally induces a G-system
$(X,G)$ naturally induces a G-system 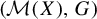 $(\mathcal {M}(X),G)$, where
$(\mathcal {M}(X),G)$, where 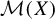 $\mathcal {M}(X)$ denotes the space of Borel probability measures on the compact metric space X endowed with the weak*-topology. A factor map
$\mathcal {M}(X)$ denotes the space of Borel probability measures on the compact metric space X endowed with the weak*-topology. A factor map 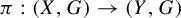 $\pi : (X,G)\to (Y,G)$ between two G-systems induces a factor map
$\pi : (X,G)\to (Y,G)$ between two G-systems induces a factor map 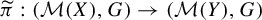 $\widetilde {\pi }:(\mathcal {M}(X),G)\to (\mathcal {M}(Y),G)$. It turns out that
$\widetilde {\pi }:(\mathcal {M}(X),G)\to (\mathcal {M}(Y),G)$. It turns out that 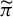 $\widetilde {\pi }$ is open if and only if
$\widetilde {\pi }$ is open if and only if 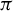 $\pi $ is open. When Y is fully supported, it is shown that
$\pi $ is open. When Y is fully supported, it is shown that 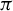 $\pi $ has relative uniformly positive entropy if and only if
$\pi $ has relative uniformly positive entropy if and only if 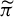 $\widetilde {\pi }$ has relative uniformly positive entropy.
$\widetilde {\pi }$ has relative uniformly positive entropy.