No CrossRef data available.
Published online by Cambridge University Press: 21 June 2022
For a subshift
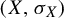 $(X, \sigma _{X})$
and a subadditive sequence
$(X, \sigma _{X})$
and a subadditive sequence
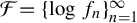 ${\mathcal F}=\{\log f_{n}\}_{n=1}^{\infty }$
on X, we study equivalent conditions for the existence of
${\mathcal F}=\{\log f_{n}\}_{n=1}^{\infty }$
on X, we study equivalent conditions for the existence of
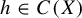 $h\in C(X)$
such that
$h\in C(X)$
such that
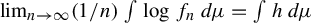 $\lim _{n\rightarrow \infty }(1/{n})\int \log f_{n}\, d\kern-1pt\mu =\int h \,d\kern-1pt\mu $
for every invariant measure
$\lim _{n\rightarrow \infty }(1/{n})\int \log f_{n}\, d\kern-1pt\mu =\int h \,d\kern-1pt\mu $
for every invariant measure
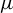 $\mu $
on X. For this purpose, we first we study necessary and sufficient conditions for
$\mu $
on X. For this purpose, we first we study necessary and sufficient conditions for
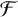 ${\mathcal F}$
to be an asymptotically additive sequence in terms of certain properties for periodic points. For a factor map
${\mathcal F}$
to be an asymptotically additive sequence in terms of certain properties for periodic points. For a factor map
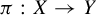 $\pi : X\rightarrow Y$
, where
$\pi : X\rightarrow Y$
, where
 $(X, \sigma _{X})$
is an irreducible shift of finite type and
$(X, \sigma _{X})$
is an irreducible shift of finite type and
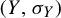 $(Y, \sigma _{Y})$
is a subshift, applying our results and the results obtained by Cuneo [Additive, almost additive and asymptotically additive potential sequences are equivalent. Comm. Math. Phys. 37 (3) (2020), 2579–2595] on asymptotically additive sequences, we study the existence of h with regard to a subadditive sequence associated to a relative pressure function. This leads to a characterization of the existence of a certain type of continuous compensation function for a factor map between subshifts. As an application, we study the projection
$(Y, \sigma _{Y})$
is a subshift, applying our results and the results obtained by Cuneo [Additive, almost additive and asymptotically additive potential sequences are equivalent. Comm. Math. Phys. 37 (3) (2020), 2579–2595] on asymptotically additive sequences, we study the existence of h with regard to a subadditive sequence associated to a relative pressure function. This leads to a characterization of the existence of a certain type of continuous compensation function for a factor map between subshifts. As an application, we study the projection
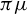 $\pi \mu $
of an invariant weak Gibbs measure
$\pi \mu $
of an invariant weak Gibbs measure
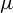 $\mu $
for a continuous function on an irreducible shift of finite type.
$\mu $
for a continuous function on an irreducible shift of finite type.