Article contents
Reeb orbits that force topological entropy
Published online by Cambridge University Press: 02 September 2021
Abstract
We develop a forcing theory of topological entropy for Reeb flows in dimension three. A transverse link L in a closed contact 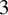 $3$
-manifold
$3$
-manifold 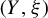 $(Y,\xi )$
is said to force topological entropy if
$(Y,\xi )$
is said to force topological entropy if 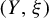 $(Y,\xi )$
admits a Reeb flow with vanishing topological entropy, and every Reeb flow on
$(Y,\xi )$
admits a Reeb flow with vanishing topological entropy, and every Reeb flow on 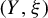 $(Y,\xi )$
realizing L as a set of periodic Reeb orbits has positive topological entropy. Our main results establish topological conditions on a transverse link L, which imply that L forces topological entropy. These conditions are formulated in terms of two Floer theoretical invariants: the cylindrical contact homology on the complement of transverse links introduced by Momin [A. Momin. J. Mod. Dyn.5 (2011), 409–472], and the strip Legendrian contact homology on the complement of transverse links, introduced by Alves [M. R. R. Alves. PhD Thesis, Université Libre de Bruxelles, 2014] and further developed here. We then use these results to show that on every closed contact
$(Y,\xi )$
realizing L as a set of periodic Reeb orbits has positive topological entropy. Our main results establish topological conditions on a transverse link L, which imply that L forces topological entropy. These conditions are formulated in terms of two Floer theoretical invariants: the cylindrical contact homology on the complement of transverse links introduced by Momin [A. Momin. J. Mod. Dyn.5 (2011), 409–472], and the strip Legendrian contact homology on the complement of transverse links, introduced by Alves [M. R. R. Alves. PhD Thesis, Université Libre de Bruxelles, 2014] and further developed here. We then use these results to show that on every closed contact 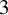 $3$
-manifold that admits a Reeb flow with vanishing topological entropy, there exist transverse knots that force topological entropy.
$3$
-manifold that admits a Reeb flow with vanishing topological entropy, there exist transverse knots that force topological entropy.
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 3
- Cited by


