Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-05T15:29:24.441Z Has data issue: false hasContentIssue false
  • English
  • Français

A rational map with infinitely many points of distinct arithmetic degrees

Part of: Birational geometry Arithmetic and non-Archimedean dynamical systems

Published online by Cambridge University Press:  12 April 2019

JOHN LESIEUTRE Open the ORCID record for JOHN LESIEUTRE [Opens in a new window]  and
MATTHEW SATRIANO
JOHN LESIEUTRE
Affiliation:
Penn State University Mathematics Department, 204 McAllister Building, University Park, State College, PA16802, USA email [email protected]
MATTHEW SATRIANO
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, ON, CanadaN2L 3G1 email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 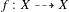be a dominant rational self-map of a smooth projective variety defined over 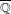$\overline{\mathbb{Q}}$. For each point 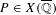$P\in X(\overline{\mathbb{Q}})$ whose forward 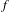$f$-orbit is well defined, Silverman introduced the arithmetic degree 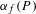$\unicode[STIX]{x1D6FC}_{f}(P)$, which measures the growth rate of the heights of the points 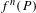$f^{n}(P)$. Kawaguchi and Silverman conjectured that 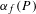$\unicode[STIX]{x1D6FC}_{f}(P)$ is well defined and that, as $P$ varies, the set of values obtained by 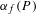$\unicode[STIX]{x1D6FC}_{f}(P)$ is finite. Based on constructions by Bedford and Kim and by McMullen, we give a counterexample to this conjecture when 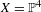$X=\mathbb{P}^{4}$.

Keywords

arithmetic dynamicsalgebraic dynamicsCremona transformations

MSC classification

Primary: 37P55: Arithmetic dynamics on general algebraic varieties
Secondary: 14E07: Birational automorphisms, Cremona group and generalizations
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 11 , November 2020 , pp. 3051 - 3055
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bedford, E. and Kim, K.. Periodicities in linear fractional recurrences: degree growth of birational surface maps. Michigan Math. J. 54(3) (2006), 647–670.CrossRefGoogle Scholar
Bedford, E. and Kim, K.. Dynamics of rational surface automorphisms: linear fractional recurrences. J. Geom. Anal. 19(3) (2009), 553–583.CrossRefGoogle Scholar
Dang, N.-B.. Degrees of iterates of rational maps on normal projective varieties. Preprint, 2017,https://arxiv.org/abs/1701.07760.Google Scholar
Kawaguchi, S.. Projective surface automorphisms of positive topological entropy from an arithmetic viewpoint. Amer. J. Math. 130(1) (2008), 159–186.CrossRefGoogle Scholar
Kawaguchi, S. and Silverman, J. H.. Examples of dynamical degree equals arithmetic degree. Michigan Math. J. 63(1) (2014), 41–63.CrossRefGoogle Scholar
Kawaguchi, S. and Silverman, J. H.. Dynamical canonical heights for Jordan blocks, arithmetic degrees of orbits, and nef canonical heights on abelian varieties. Trans. Amer. Math. Soc. 368(7) (2016), 5009–5035.CrossRefGoogle Scholar
Kawaguchi, S. and Silverman, J. H.. On the dynamical and arithmetic degrees of rational self-maps of algebraic varieties. J. Reine Angew. Math. 713 (2016), 21–48.Google Scholar
McMullen, C. T.. Dynamics on blowups of the projective plane. Publ. Math. Inst. Hautes Études Sci. 105 (2007), 49–89.CrossRefGoogle Scholar
Matsuzawa, Y., Sano, K. and Shibata, T.. Arithmetic degrees and dynamical degrees of endomorphisms on surfaces. Algebra Number Theory 12(7) (2018), 1635–1657.CrossRefGoogle Scholar
Silverman, J. H.. Dynamical degree, arithmetic entropy, and canonical heights for dominant rational self-maps of projective space. Ergod. Th. & Dynam. Sys. 34(2) (2014), 647–678.CrossRefGoogle Scholar
Zhang, D.-Q.. The g-periodic subvarieties for an automorphism g of positive entropy on a compact Kähler manifold. Adv. Math. 223(2) (2010), 405–415.CrossRefGoogle Scholar