Hostname: page-component-6bf8c574d5-b4m5d Total loading time: 0 Render date: 2025-02-21T11:59:19.888Z Has data issue: false hasContentIssue false
  • English
  • Français

Quasisymmetric orbit-flexibility of multicritical circle maps

Part of: Low-dimensional dynamical systems Smooth dynamical systems: general theory

Published online by Cambridge University Press:  30 September 2021

EDSON DE FARIA Open the ORCID record for EDSON DE FARIA [Opens in a new window]  and
PABLO GUARINO Open the ORCID record for PABLO GUARINO [Opens in a new window]
EDSON DE FARIA
Affiliation:
Instituto de Matemática e Estatística, Universidade de São Paulo, Brazil (e-mail: [email protected])
PABLO GUARINO*
Affiliation:
Instituto de Matemática e Estatística, Universidade Federal Fluminense, Brazil
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Two given orbits of a minimal circle homeomorphism f are said to be geometrically equivalent if there exists a quasisymmetric circle homeomorphism identifying both orbits and commuting with f. By a well-known theorem due to Herman and Yoccoz, if f is a smooth diffeomorphism with Diophantine rotation number, then any two orbits are geometrically equivalent. It follows from the a priori bounds of Herman and Świątek, that the same holds if f is a critical circle map with rotation number of bounded type. By contrast, we prove in the present paper that if f is a critical circle map whose rotation number belongs to a certain full Lebesgue measure set in 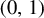$(0,1)$ , then the number of equivalence classes is uncountable (Theorem 1.1). The proof of this result relies on the ergodicity of a two-dimensional skew product over the Gauss map. As a by-product of our techniques, we construct topological conjugacies between multicritical circle maps which are not quasisymmetric, and we show that this phenomenon is abundant, both from the topological and measure-theoretical viewpoints (Theorems 1.6 and 1.8).

Keywords

critical circle mapsquasisymmetric orbit-flexibilityskew product

MSC classification

Primary: 37E10: Maps of the circle
Secondary: 37E20: Universality, renormalization 37C40: Smooth ergodic theory, invariant measures
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 11 , November 2022 , pp. 3271 - 3310
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Astala, K., Iwaniec, T. and Martin, G.. Elliptic Partial Differential Equations and Quasiconformal Mappings in the Plane. Princeton University Press, Princeton, NJ, 2009.Google Scholar
Avila, A.. On rigidity of critical circle maps. Bull. Braz. Math. Soc. 44 (2013), 611–619.CrossRefGoogle Scholar
Avila, A., Cheraghi, D. and Eliad, A.. Analytic maps of parabolic and elliptic type with trivial centralisers. Ann. Inst. H. Poincaré Anal. Non Linéaire, to appear, Preprint, 2020, arXiv:2003.13336.Google Scholar
Buzzi, J.. Absolutely continuous invariant probability measures for arbitrary expanding piecewise $\mathbb{R}$ -analytic mappings of the plane. Ergod. Th. & Dynam. Sys. 20 (2000), 697–708.CrossRefGoogle Scholar
Clark, T. and van Strien, S.. Quasisymmetric rigidity in one-dimensional dynamics. Preprint, 2018, arXiv:1805.092843.Google Scholar
de Faria, E.. Proof of universality for critical circle mappings. PhD Thesis, City University of New York, 1992.Google Scholar
de Faria, E.. Asymptotic rigidity of scaling ratios for critical circle mappings. Ergod. Th. & Dynam. Sys. 19 (1999), 995–1035.CrossRefGoogle Scholar
de Faria, E. and de Melo, W.. Rigidity of critical circle mappings I. J. Eur. Math. Soc. (JEMS) 1 (1999), 339–392.CrossRefGoogle Scholar
de Faria, E. and de Melo, W.. Rigidity of critical circle mappings II. J. Amer. Math. Soc. 13 (2000), 343–370.CrossRefGoogle Scholar
de Faria, E. and de Melo, W.. Mathematical Tools for One-Dimensional Dynamics. Cambridge University Press, Cambridge, 2008.CrossRefGoogle Scholar
de Faria, E. and Guarino, P.. Real bounds and Lyapunov exponents. Discrete Contin. Dyn. Syst. 36 (2016), 1957–1982.Google Scholar
de Faria, E. and Guarino, P.. There are no $\sigma$ -finite absolutely continuous invariant measures for multicritical circle maps. Nonlinearity 34 (2021), 6727.CrossRefGoogle Scholar
Estevez, G. and de Faria, E.. Real bounds and quasisymmetric rigidity of multicritical circle maps. Trans. Amer. Math. Soc. 370 (2018), 5583–5616.CrossRefGoogle Scholar
Estevez, G., de Faria, E. and Guarino, P.. Beau bounds for multicritical circle maps. Indag. Math. 29 (2018), 842–859.CrossRefGoogle Scholar
Estevez, G. and Guarino, P.. Renormalization of multicritical circle maps. Preprint.Google Scholar
Guarino, P.. Rigidity conjecture for ${C}^3$ critical circle maps. PhD Thesis, Instituto de Matemática Pura e Aplicada, 2012.Google Scholar
Guarino, P. and de Melo, W.. Rigidity of smooth critical circle maps. J. Eur. Math. Soc. (JEMS) 19 (2017), 1729–1783.CrossRefGoogle Scholar
Guarino, P., Martens, M. and de Melo, W.. Rigidity of critical circle maps. Duke Math. J. 167 (2018), 2125–2188.CrossRefGoogle Scholar
Herman, M.. Sur la conjugaison différentiable des difféomorphismes du cercle à des rotations. Publ. Math. Inst. Hautes Études Sci. 49 (1979), 5–234.CrossRefGoogle Scholar
Herman, M.. Conjugaison quasi-simétrique des homéomorphismes du cercle à des rotations, manuscript, 1988 (see also the translation by A. Chéritat, Quasisymmetric conjugacy of analytic circle homeomorphisms to rotations, available at www.math.univ-toulouse.fr/~cheritat/Herman/e_herman.html).Google Scholar
Katznelson, Y. and Ornstein, D.. The differentiability of the conjugation of certain diffeomorphisms of the circle. Ergod. Th. & Dynam. Sys. 9 (1989), 643–680.CrossRefGoogle Scholar
Khanin, K. and Teplinsky, A.. Robust rigidity for circle diffeomorphisms with singularities. Invent. Math. 169 (2007), 193–218.CrossRefGoogle Scholar
Khinchin, A. Ya.. Continued Fractions. Dover Publications Inc., Mineola, NY, 1997 (reprint of the 1964 translation).Google Scholar
Khmelev, D. and Yampolsky, M.. The rigidity problem for analytic critical circle maps. Mosc. Math. J. 6 (2006), 317–351.CrossRefGoogle Scholar
Lanford, O. E.. Renormalization group methods for critical circle mappings with general rotation number. VIIIth International Congress on Mathematical Physics (Marseille, 1986). World Scientific, Singapore, 1987, pp. 532–536.Google Scholar
Lanford, O. E.. Renormalization group methods for circle mappings. Nonlinear Evolution and Chaotic Phenomena (NATO Advanced Science Institutes Series B: Physics, 176). Plenum, New York, 1988, pp. 25–36.Google Scholar
Lang, S.. Introduction to Diophantine Approximations, new expanded edition. Springer, New York, 1995.CrossRefGoogle Scholar
Martens, M., Palmisano, L. and Winckler, B.. The rigidity conjecture. Indag. Math. 29 (2018), 825–830.CrossRefGoogle Scholar
Świa̧tek, G.. Rational rotation numbers for maps of the circle. Comm. Math. Phys. 119 (1988), 109–128.CrossRefGoogle Scholar
Trujillo, F.. Hausdorff dimension of invariant measures of multicritical circle maps. Ann. Henri Poincaré 21 (2020), 2861–2875.CrossRefGoogle Scholar
Tsujii, M.. Absolutely continuous invariant measures for expanding piecewise linear maps. Invent. Math. 143 (2001), 349–373.CrossRefGoogle Scholar
Yampolsky, M.. Complex bounds for renormalization of critical circle maps. Ergod. Th. & Dynam. Sys. 19 (1999), 227–257.CrossRefGoogle Scholar
Yampolsky, M.. The attractor of renormalization and rigidity of towers of critical circle maps. Comm. Math. Phys. 218 (2001), 537–568.CrossRefGoogle Scholar
Yampolsky, M.. Hyperbolicity of renormalization of critical circle maps. Publ. Math. Inst. Hautes Études Sci. 96 (2002), 1–41.CrossRefGoogle Scholar
Yampolsky, M.. Renormalization horseshoe for critical circle maps. Comm. Math. Phys. 240 (2003), 75–96.CrossRefGoogle Scholar
Yampolsky, M.. Renormalization of bi-cubic circle maps. C. R. Math. Rep. Acad. Sci. Canada 41 (2019), 57–83.Google Scholar
Yoccoz, J.-C.. Il n’y a pas de contre-exemple de Denjoy analytique. C. R. Acad. Sci. Paris 298 (1984), 141–144.Google Scholar
Yoccoz, J.-C.. Conjugaison différentiable des difféomorphismes du cercle dont le nombre de rotation vérifie une condition diophantienne. Ann. Sci. Éc. Norm. Supér. (4) 17 (1984), 333–359.CrossRefGoogle Scholar
Yoccoz, J.-C.. Centralisateurs et conjugaison differentiable des difféomorphismes du cercle. Thèse d’Etat, Université Paris Sud, 1985.Google Scholar
Yoccoz, J.-C.. Centralisateurs et conjugaison différentiable des difféomorphismes du cercle. Astérisque 231 (1995), 89–242.Google Scholar
Zakeri, S.. Dynamics of cubic Siegel polynomials. Comm. Math. Phys. 206 (1999), 185–233.CrossRefGoogle Scholar