Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-28T03:08:52.134Z Has data issue: false hasContentIssue false
  • English
  • Français

A proof of the Kuramoto conjecture for a bifurcation structure of the infinite-dimensional Kuramoto model

Published online by Cambridge University Press:  11 October 2013

HAYATO CHIBA
HAYATO CHIBA*
Affiliation:
Institute of Mathematics, Kyushu University, Fukuoka, 819-0395, Japan email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The Kuramoto model is a system of ordinary differential equations for describing synchronization phenomena defined as coupled phase oscillators. In this paper, a bifurcation structure of the infinite-dimensional Kuramoto model is investigated. A purpose here is to prove the bifurcation diagram of the model conjectured by Kuramoto in 1984; if the coupling strength 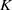$K$ between oscillators, which is a parameter of the system, is smaller than some threshold 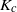${K}_{c} $, the de-synchronous state (trivial steady state) is asymptotically stable, while if 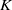$K$ exceeds 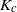${K}_{c} $, a non-trivial stable solution, which corresponds to the synchronization, bifurcates from the de-synchronous state. One of the difficulties in proving the conjecture is that a certain non-selfadjoint linear operator, which defines a linear part of the Kuramoto model, has the continuous spectrum on the imaginary axis. Hence, the standard spectral theory is not applicable to prove a bifurcation as well as the asymptotic stability of the steady state. In this paper, the spectral theory on a space of generalized functions is developed with the aid of a rigged Hilbert space to avoid the continuous spectrum on the imaginary axis. Although the linear operator has an unbounded continuous spectrum on a Hilbert space, it is shown that it admits a spectral decomposition consisting of a countable number of eigenfunctions on a space of generalized functions. The semigroup generated by the linear operator will be estimated with the aid of the spectral theory on a rigged Hilbert space to prove the linear stability of the steady state of the system. The center manifold theory is also developed on a space of generalized functions. It is proved that there exists a finite-dimensional center manifold on a space of generalized functions, while a center manifold on a Hilbert space is of infinite dimension because of the continuous spectrum on the imaginary axis. These results are applied to the stability and bifurcation theory of the Kuramoto model to obtain a bifurcation diagram conjectured by Kuramoto.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 3 , May 2015 , pp. 762 - 834
Copyright
© Cambridge University Press, 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acebrón, J. A., Bonilla, L. L., Vicente, C. J. P., Ritort, F. and Spigler, R.. The Kuramoto model: a simple paradigm for synchronization phenomena. Rev. Mod. Phys. 77 (2005), 137–185.Google Scholar
Acebrón, J. A. and Bonilla, L. L.. Asymptotic description of transients and synchronized states of globally coupled oscillators. Phys. D 114 (3–4) (1998), 296–314.Google Scholar
Ahlfors, L. V.. Complex Analysis. An Introduction to the Theory of Analytic Functions of One Complex Variable. McGraw-Hill Book Co, New York, 1978.Google Scholar
Balmforth, N. J. and Sassi, R.. A shocking display of synchrony. Phys. D 143 (1–4) (2000), 21–55.CrossRefGoogle Scholar
Bates, P. W. and Jones, C. K. R. T.. Invariant manifolds for semilinear partial differential equations. Dynamics Reported. Vol. 2. John Wiley, Chichester, 1989, pp. 1–38.Google Scholar
Bonilla, L. L., Neu, J. C. and Spigler, R.. Nonlinear stability of incoherence and collective synchronization in a population of coupled oscillators. J. Stat. Phys. 67 (1–2) (1992), 313–330.Google Scholar
Bonilla, L. L., Pérez Vicente, C. J. and Spigler, R.. Time-periodic phases in populations of nonlinearly coupled oscillators with bimodal frequency distributions. Phys. D 113 (1) (1998), 79–97.Google Scholar
Chen, X.-Y., Hale, J. K. and Bin, T.. Invariant foliations for ${C}^{1} $ semigroups in Banach spaces. J. Differential Equations 139 (2) (1997), 283–318.Google Scholar
Chiba, H. and Nishikawa, I.. Center manifold reduction for a large population of globally coupled phase oscillators. Chaos 21 (2011).CrossRefGoogle ScholarPubMed
Chiba, H.. Continuous limit and the moments system for the globally coupled phase oscillators. Discrete. Contin. Dyn. Syst. 33 (2013), 1891–1903.Google Scholar
Chiba, H. and Pazó, D.. Stability of an $[N/ 2] $-dimensional invariant torus in the Kuramoto model at small coupling. Phys. D 238 (2009), 1068–1081.CrossRefGoogle Scholar
Crawford, J. D.. Amplitude expansions for instabilities in populations of globally-coupled oscillators. J. Stat. Phys. 74 (5–6) (1994), 1047–1084.Google Scholar
Crawford, J. D.. Scaling and singularities in the entrainment of globally coupled oscillators. Phys. Rev. Lett. 74 (1995), 4341–4344.Google Scholar
Crawford, J. D. and Davies, K. T. R.. Synchronization of globally coupled phase oscillators: singularities and scaling for general couplings. Phys. D 125 (1–2) (1999), 1–46.Google Scholar
Gelfand, I. M. and Shilov, G. E.. Generalized functions. Spaces of Fundamental and Generalized Functions. Vol. 2. Academic Press, New York–London, 1968.Google Scholar
Gelfand, I. M. and Vilenkin, N. Ya.. Generalized functions. Applications of Harmonic Analysis. Vol. 4. Academic Press, New York–London, 1964.Google Scholar
Grothendieck, A.. Topological Vector Spaces. Gordon and Breach Science Publishers, New York–London–Paris, 1973.Google Scholar
Hille, E. and Phillips, R. S.. Functional Analysis and Semigroups. American Mathematical Society, Providence, RI, 1957.Google Scholar
Kato, T.. Perturbation Theory for Linear Operators. Springer, Berlin, 1995.Google Scholar
Komatsu, H.. Projective and injective limits of weakly compact sequences of locally convex spaces. J. Math. Soc. Japan 19 (1967), 366–383.CrossRefGoogle Scholar
Krisztin, T.. Invariance and noninvariance of center manifolds of time-$t$ maps with respect to the semiflow. SIAM J. Math. Anal. 36 (3) (2004/05), 717–739.CrossRefGoogle Scholar
Kuramoto, Y.. Self-entrainment of a population of coupled non-linear oscillators. International Symposium on Mathematical Problems in Theoretical Physics (Lecture Notes in Physics, 39). Springer, Berlin, 1975, pp. 420–422.Google Scholar
Kuramoto, Y.. Chemical Oscillations, Waves, and Turbulence (Springer Series in Synergetics, 19). Springer-Verlag, Berlin, 1984.Google Scholar
Maistrenko, Y., Popovych, O., Burylko, O. and Tass, P. A.. Mechanism of desynchronization in the finite-dimensional Kuramoto model. Phys. Rev. Lett. 93 (2004).Google Scholar
Maistrenko, Y. L., Popovych, O. V. and Tass, P. A.. Chaotic attractor in the Kuramoto model. Internat. J. Bifur. Chaos Appl. Sci. Engrg. 15 (2005), 3457–3466.CrossRefGoogle Scholar
Maurin, K.. General Eigenfunction Expansions and Unitary Representations of Topological Groups. Polish Scientific Publishers, Warsaw, 1968.Google Scholar
Martens, E. A., Barreto, E., Strogatz, S. H., Ott, E., So, P. and Antonsen, T. M.. Exact results for the Kuramoto model with a bimodal frequency distribution. Phys. Rev. E 79 (2009).CrossRefGoogle ScholarPubMed
Marvel, S. A., Mirollo, R. E. and Strogatz, S. H.. Identical phase oscillators with global sinusoidal coupling evolve by Mobius group action. Chaos 19 (2009).Google Scholar
Mirollo, R. E. and Strogatz, S. H.. Amplitude death in an array of limit-cycle oscillators. J. Stat. Phys. 60 (1–2) (1990), 245–262.Google Scholar
Mirollo, R. and Strogatz, S. H.. The spectrum of the partially locked state for the Kuramoto model. J. Nonlinear Sci. 17 (4) (2007), 309–347.Google Scholar
Ott, E. and Antonsen, T. M.. Low dimensional behavior of large systems of globally coupled oscillators. Chaos 18 (3) (2008).Google Scholar
Ott, E. and Antonsen, T. M.. Long time evolution of phase oscillator systems. Chaos 19 (2) (2009).CrossRefGoogle ScholarPubMed
Pikovsky, A., Rosenblum, M. and Kurths, J.. Synchronization: A Universal Concept in Nonlinear Sciences. Cambridge University Press, Cambridge, 2001.Google Scholar
Reed, M. and Simon, B.. Methods of Modern Mathematical Physics IV: Analysis of Operators. Academic Press, New York–London, 1978.Google Scholar
Sanders, J. A. and Verhulst, F.. Averaging Methods in Nonlinear Dynamical Systems. Springer-Verlag, New York, 1985.Google Scholar
Shohat, J. A. and Tamarkin, J. D.. The Problem of Moments. American Mathematical Society, New York, 1943.CrossRefGoogle Scholar
Stein, E. M. and Weiss, G.. Introduction to Fourier Analysis on Euclidean Spaces. Princeton University Press, Princeton, 1971.Google Scholar
Strogatz, S. H.. From Kuramoto to Crawford: exploring the onset of synchronization in populations of coupled oscillators. Phys. D 143 (1–4) (2000), 1–20.Google Scholar
Strogatz, S. H. and Mirollo, R. E.. Stability of incoherence in a population of coupled oscillators. J. Stat. Phys. 63 (3–4) (1991), 613–635.Google Scholar
Strogatz, S. H., Mirollo, R. E. and Matthews, P. C.. Coupled nonlinear oscillators below the synchronization threshold: relaxation by generalized Landau damping. Phys. Rev. Lett. 68 (18) (1992), 2730–2733.CrossRefGoogle ScholarPubMed
Titchmarsh, E. C.. Introduction to the Theory of Fourier Integrals. Chelsea Publishing Co, New York, 1986.Google Scholar
Tréves, F.. Topological Vector Spaces, Distributions and Kernels. Academic Press, New York–London, 1967.Google Scholar
Vanderbauwhede, A. and Iooss, G.. Center manifold theory in infinite dimensions. Dynamics Reported Expositions in Dynamical Systems, 1. Springer, Berlin, 1992.Google Scholar
Vilenkin, N. J.. Special Functions and the Theory of Group Representations. American Mathematical Society, Providence, RI, 1968.Google Scholar
Yosida, K.. Functional Analysis. Springer-Verlag, Berlin, 1995.Google Scholar