Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-16T15:27:39.083Z Has data issue: false hasContentIssue false
  • English
  • Français

Product set phenomena for measured groups

Published online by Cambridge University Press:  04 May 2017

MICHAEL BJÖRKLUND
MICHAEL BJÖRKLUND*
Affiliation:
Department of Mathematics, Chalmers University of Technology, Gothenburg, Sweden email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We strengthen and extend in this paper some recent results by Di Nasso, Goldbring, Jin, Leth, Lupini and Mahlburg on piecewise syndeticity of product sets in countable amenable groups to general countable measured groups. We also address several fundamental differences between the behavior of products of ‘large’ sets in Liouville and non-Liouville measured groups. As a (very) special case of our main results, we show that if 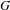$G$ is a free group of finite rank, and $A$ and 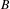$B$ are ‘spherically large’ subsets of 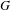$G$, then there exists a finite set 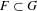$F\subset G$ such that 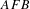$AFB$ is thick. The position of the set $F$ is curious, but seems to be necessary; in fact, we can produce left thick sets 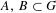$A,B\subset G$ such that 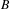$B$ is ‘spherically large’, but 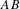$AB$ is not piecewise syndetic. On the other hand, if $A$ is spherically large, then 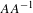$AA^{-1}$ is always piecewise syndetic and piecewise left syndetic. However, contrary to what happens for amenable groups, $AA^{-1}$ may fail to be syndetic. The same phenomena occur for many other (even amenable, but non-Liouville) measured groups. Our proofs are based on some ergodic-theoretical results concerning stationary actions which should be of independent interest.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 8 , December 2018 , pp. 2913 - 2941
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aliprantis, C. D. and Border, K. C.. Infinite Dimensional Analysis. A Hitchhiker’s Guide, 3rd edn. Springer, Berlin, 2006.Google Scholar
Bader, U. and Shalom, Y.. Factor and normal subgroup theorems for lattices in products of groups. Invent. Math. 163(2) (2006), 415–454.Google Scholar
Beiglböck, M., Bergelson, V. and Fish, A.. Sumset phenomenon in countable amenable groups. Adv. Math. 223(2) (2010), 416–432.Google Scholar
Björklund, M.. Random walks on countable groups. Israel J. Math. to appear.Google Scholar
Björklund, M. and Fish, A.. Product set phenomena for countable groups. Adv. Math. 275 (2015), 47–113.Google Scholar
Brofferio, S.. The Poisson boundary of random rational affinities. Ann. Inst. Fourier (Grenoble) 56(2) (2006), 499–515.Google Scholar
Di Nasso, M. and Lupini, M.. Nonstandard analysis and the sumset phenomenon in arbitrary amenable groups. Illinois J. Math. 58(1) (2014), 11–25.Google Scholar
Di Nasso, M., Goldbring, I., Leth, Jin R., Lupini, M. and Mahlburg, K.. High density piecewise syndeticity of sumsets. Adv. Math. 278 (2015), 1–33.Google Scholar
Di Nasso, M., Goldbring, I., Leth, Jin R., Lupini, M. and Mahlburg, K.. High density piecewise syndeticity of product sets in amenable groups. J. Symbolic Logic 81(4) (2015), 1555–1562.Google Scholar
Einsiedler, M. and Ward, T.. Ergodic Theory with a View Towards Number Theory (Graduate Texts in Mathematics, 259) . Springer, London, 2011.Google Scholar
Følner, E.. On groups with full Banach mean value. Math. Scand. 3 (1955), 243–254.Google Scholar
Frisch, J., Schlank, T. and Tamuz, O.. Normal amenable subgroups of the automorphism group of the full shift. Preprint, 2015, https://arxiv.org/abs/1512.00587.Google Scholar
Furstenberg, H.. Random Walks and Discrete Subgroups of Lie Groups (Advances in Probability and Related Topics, 1) . Dekker, New York, 1971, pp. 1–63.Google Scholar
Furstenberg, H. and Glasner, E.. Stationary dynamical systems. Dynamical Numbers – Interplay Between Dynamical Systems and Number Theory (Contemporary Mathematics, 532) . American Mathematical Society, Providence, RI, 2010, pp. 1–28.Google Scholar
Furstenberg, H. and Glasner, E.. Recurrence for stationary group actions. From Fourier Analysis and Number Theory to Radon Transforms and Geometry (Developments in Mathematics, 28) . Springer, New York, 2013, pp. 283–291.Google Scholar
Glasner, S.. Proximal Flows (Lecture Notes in Mathematics, 517) . Springer, Berlin, 1976.Google Scholar
Jaworski, W.. Strongly approximately transitive group actions, the Choquet–Deny theorem, and polynomial growth. Pacific J. Math. 165(1) (1994), 115–129.Google Scholar
Jin, R.. The sumset phenomenon. Proc. Amer. Math. Soc. 130(3) (2002), 855–861.Google Scholar
Kaimanovich, V.. SAT actions and ergodic properties of the horosphere foliation. Rigidity in Dynamics and Geometry (Special Semester, Cambridge, UK, 5 January–7 July 2000). Eds. Burger, M. and Iozzi, A.. Springer, Berlin, 2002, pp. 261–282.Google Scholar
Kaimanovich, V. and Vershik, A.. Random walks on discrete groups: boundary and entropy. Ann. Probab. 11(3) (1983), 457–490.Google Scholar
Rosenblatt, J.. Ergodic and mixing random walks on locally compact groups. Math. Ann. 257(1) (1981), 31–42.Google Scholar