Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T09:54:19.419Z Has data issue: false hasContentIssue false
  • English
  • Français

Prime Poisson suspensions

Published online by Cambridge University Press:  04 August 2014

FRANÇOIS PARREAU  and
EMMANUEL ROY
FRANÇOIS PARREAU
Affiliation:
Laboratoire Analyse Géométrie et Applications, UMR 7539, Université Paris 13, 99 avenue J.B. Clément, F-93430 Villetaneuse, France email [email protected], [email protected]
EMMANUEL ROY
Affiliation:
Laboratoire Analyse Géométrie et Applications, UMR 7539, Université Paris 13, 99 avenue J.B. Clément, F-93430 Villetaneuse, France email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We establish a necessary and sufficient condition for a Poisson suspension to be prime. The proof is based on the Fock space structure of the 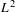$L^{2}$-space of the Poisson suspension. We give examples of explicit infinite measure-preserving systems, in particular of non-singular compact group rotations that give rise to prime Poisson suspensions. We also compare some properties of so far known prime transformations with those of our examples, showing that these examples are new.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 7 , October 2015 , pp. 2216 - 2230
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aaronson, J. and Nadkarni, M.. L ∞ eigenvalues and L 2 spectra of non-singular transformations. Proc. Lond. Math. Soc. 55 (1987), 538–570.CrossRefGoogle Scholar
Brown, G. and Moran, W.. On orthogonality of Riesz products. Proc. Cambridge Phil. Soc. 76 ( 1974), 173–181.CrossRefGoogle Scholar
del Junco, A.. A family of counterexamples in ergodic theory. Israel J. Math. 44(2) (1983), 160–188.CrossRefGoogle Scholar
del Junco, A. and Danilenko, A. I.. Cut-and-stack simple weakly mixing map with countably many prime factors. Proc. Amer. Math. Soc. 136 (2008), 2463–2472.Google Scholar
del Junco, A., Rahe, M. and Swanson, L.. Chacon’s automorphism has minimal self-joinings. J. Anal. Math. 37 (1980), 276–284.CrossRefGoogle Scholar
del Junco, A. and Rudolph, D. J.. On ergodic actions whose self-joinings are graphs. Ergod. Th. & Dynam. Sys. 7(4) (1987), 531–557.CrossRefGoogle Scholar
del Junco, A. and Rudolph, D. J.. A rank one, rigid, simple, prime map. Ergod. Th. & Dynam. Sys. 7 ( 1987), 229–247.CrossRefGoogle Scholar
Derriennic, Y., Frcaczek, K., Lemańczyk, M. and Parreau, F.. Ergodic automorphisms whose weak closure of off-diagonal measures consists of ergodic self-joinings. Colloq. Math. 110 (2008), 81–115.CrossRefGoogle Scholar
Glasner, E. and Weiss, B.. A simple weakly mixing transformation with non-unique prime factors. Amer. J. Math. 116(2) (1994), 361–375.CrossRefGoogle Scholar
Host, B., Méla, J.-F. and Parreau, F.. Analyse harmonique des mesures. Astérisque 135–136 (1986).Google Scholar
Host, B., Méla, J.-F. and Parreau, F.. Non-singular transformations and spectral theory. Bull. Soc. Math. France 119 (1991), 33–90.CrossRefGoogle Scholar
King, J. L.. The commutant is the weak closure of the powers, for rank-1 transformations. Ergod. Th. & Dynam. Sys. 6(3) (1986), 363–384.CrossRefGoogle Scholar
King, J. L.. Joining-rank and the structure of finite-rank mixing transformations. J. Anal. Math. 51 ( 1998), 182–227.CrossRefGoogle Scholar
Kulaga-Przymus, J. and Parreau, F.. Disjointness properties for cartesian products of weakly mixing systems. Colloq. Math. 128(2) ( 2012), 153–177.CrossRefGoogle Scholar
Last, G. and Penrose, M.. Poisson process Fock space representation, chaos expansion and covariance inequalities. Probab. Theory Related Fields 150(3–4) (2011), 663–690.CrossRefGoogle Scholar
Lemańczyk, M. and Parreau, F.. Lifting mixing properties by Rokhlin cocycles. Ergod. Th. & Dynam. Sys. 32(2) (2011), 763–784.CrossRefGoogle Scholar
Lemańczyk, M., Parreau, F. and Roy, E.. Joining primeness and disjointness from infinitely divisible systems. Proc. Amer. Math. Soc. 139 (2011), 185–199.CrossRefGoogle Scholar
Lemańczyk, M., Parreau, F. and Thouvenot, J.-P.. Gaussian automorphisms whose ergodic self-joinings are Gaussian. Fund. Math. 164 (2000), 253–293.CrossRefGoogle Scholar
Liebscher, V.. On the isomorphism of Poisson space and symmetric Fock space. Quantum Probability and Related Topics Accardi, L. World Scientific, Singapore, 1994.Google Scholar
Mecke, J.. Stationäre zufällige maauf lokalkompakten abelschen gruppen. Z. Wahrsch. Verw. Gebiete. 9 (1967), 36–58.CrossRefGoogle Scholar
Ornstein, D. S.. On the root problem in ergodic theory. Proc. Sixth Berkeley Symp. on Math. Statist and Prob., vol. 2. University of California Press, Berkeley, CA, 1972, pp. 347–356.Google Scholar
Peyrière, J.. Etude de quelques propriétés des produits de Riesz. Ann. Inst. Fourier 25(2) (1975), 127–169.CrossRefGoogle Scholar
Polit, S.. Weakly isomorphic maps need not be isomorphic. PhD Thesis, Stanford, 1974.Google Scholar
Roy, E.. Poisson suspensions and infinite ergodic theory. Ergod. Th. & Dynam. Sys. 29(2) (2009), 667–683.CrossRefGoogle Scholar
Rudolph, D. J.. Fundamentals of Measurable Dynamics. Oxford University Press, Oxford, 1990.Google Scholar
Ryzhikov, V. V.. Mixing, rank and minimal self-joining of actions with invariant measure. Mat. Sb. 183(3) (1992), 133–160.Google Scholar
Ryzhikov, V. V.. On mixing rank one infinite transformations. Preprint, 2011, arXiv:11064655.Google Scholar
Thouvenot, J.-P.. Some properties and applications of joinings in ergodic theory. Ergodic Theory and its Connections with Harmonic Analysis (Alexandria, 1993) (London Mathematical Society Lecture Note Series, 205). Cambridge University Press, Cambridge, 1995, pp. 207–235.CrossRefGoogle Scholar
Veech, W. A.. A criterion for a process to be prime. Monatsh. Math. 94(4) (1982), 335–341.CrossRefGoogle Scholar