Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T01:19:48.606Z Has data issue: false hasContentIssue false
  • English
  • Français

Positive area and inaccessible fixed points for hedgehogs

Published online by Cambridge University Press:  13 April 2015

KINGSHOOK BISWAS
KINGSHOOK BISWAS*
Affiliation:
Ramakrishna Mission Vivekananda University, Belur Math, WB-711202, India email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 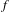$f$ be a germ of holomorphic diffeomorphism with an irrationally indifferent fixed point at the origin in 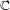$\mathbb{C}$ (i.e. 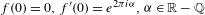$f(0)=0,f^{\prime }(0)=e^{2{\it\pi}i{\it\alpha}},{\it\alpha}\in \mathbb{R}-\mathbb{Q}$). Perez-Marco showed the existence of a unique family of non-trivial invariant full continua containing the fixed point called Siegel compacta. When 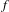$f$ is non-linearizable (i.e. not holomorphically conjugate to the rigid rotation 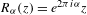$R_{{\it\alpha}}(z)=e^{2{\it\pi}i{\it\alpha}}z$) the invariant compacts obtained are called hedgehogs. Perez-Marco developed techniques for the construction of examples of non-linearizable germs [Fixed points and circle maps. Acta Math. 179(2) (1997), 243–294]; these were used by the author to construct hedgehogs of Hausdorff dimension one, and adapted by Cheritat [Relatively compact Siegel disks with non-locally connected boundaries, Preprint, 2009] to construct Siegel disks with pseudo-circle boundaries. We use these techniques to construct hedgehogs of positive area and hedgehogs with inaccessible fixed points.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 6 , September 2016 , pp. 1839 - 1850
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Buff, X. and Cheritat, A.. Quadratic Julia sets with positive area. Ann. of Math. (2) 176 (2012), 673–746.Google Scholar
Biswas, K.. Smooth combs inside hedgehogs. Discrete Contin. Dyn. Syst. 12(5) (2005), 853–880.Google Scholar
Biswas, K.. Hedgehogs of Hausdorff dimension one. Ergod. Th. & Dynam. Sys. 28(6) (2008), 1713–1727.Google Scholar
Brjuno, A. D.. Analytical form of differential equations. Trans. Moscow Math. Soc. 25 (1971), 131–288.Google Scholar
Cheritat, A.. Relatively compact Siegel disks with non-locally connected boundaries. Math. Annal. 349(3) (2011), 529–542.Google Scholar
Perez-Marco, R.. Sur les dynamiques holomorphes non-linearisables et une conjecture de V. I. Arnold. Ann. Sci. Éc. Norm. Supér. 26 (1993), 565–644.Google Scholar
Perez-Marco, R.. Topology of Julia sets and hedgehogs. Preprint, Université de Paris-Sud, 1994.Google Scholar
Perez-Marco, R.. Uncountable number of symmetries for non-linearisable holomorphic dynamics. Invent. Math. 119 (1995), 67–127.Google Scholar
Perez-Marco, R.. Hedgehogs dynamics. Preprint, University of California, Los Angeles, 1996.Google Scholar
Perez-Marco, R.. Fixed points and circle maps. Acta Math. 179(2) (1997), 243–294.Google Scholar
Perez-Marco, R.. Siegel disks with smooth boundary. Preprint, 2000.Google Scholar
Siegel, C. L.. Iteration of analytic functions. Ann. Math. 43 (1942), 807–812.Google Scholar
Yoccoz, J. C.. Petits diviseurs en dimension 1. Astérisque 231 (1995).Google Scholar