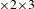Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T02:17:53.875Z Has data issue: false hasContentIssue false
  • English
  • Français

A polynomial-exponential variation of Furstenberg’s $\times 2\times 3$ theorem

Part of: Topological dynamics Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  19 December 2018

M. ABRAMOFF  and
D. BEREND Open the ORCID record for D. BEREND [Opens in a new window]
M. ABRAMOFF
Affiliation:
Department of Mathematics, Ben-Gurion University, Beer Sheva 84105, Israel email [email protected]
D. BEREND
Affiliation:
Departments of Mathematics and Computer Science, Ben-Gurion University, Beer Sheva 84105, Israel email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Furstenberg’s 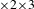$\times 2\times 3$ theorem asserts that the double sequence 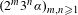$(2^{m}3^{n}\unicode[STIX]{x1D6FC})_{m,n\geq 1}$ is dense modulo one for every irrational $\unicode[STIX]{x1D6FC}$. The same holds with $2$ and $3$ replaced by any two multiplicatively independent integers. Here we obtain the same result for the sequences 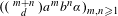$((\begin{smallmatrix}m+n\\ d\end{smallmatrix})a^{m}b^{n}\unicode[STIX]{x1D6FC})_{m,n\geq 1}$ for any non-negative integer 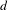$d$ and irrational $\unicode[STIX]{x1D6FC}$, and for the sequence 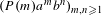$(P(m)a^{m}b^{n})_{m,n\geq 1}$, where $P$ is any polynomial with at least one irrational coefficient. Similarly to Furstenberg’s theorem, both results are obtained by considering appropriate dynamical systems.

Keywords

density modulo 1topological dynamicsFurstenberg’s diophantine theorem

MSC classification

Primary: 11J71: Distribution modulo one 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 7 , July 2020 , pp. 1729 - 1737
Copyright
© Cambridge University Press, 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berend, D.. Multi-invariant sets on tori. Trans. Amer. Math. Soc. 280 (1983), 509–532.Google Scholar
Berend, D.. Multi-invariant sets on compact abelian groups. Trans. Amer. Math. Soc. 286 (1984), 505–535.Google Scholar
Berend, D.. Minimal sets on tori. Ergod. Th. & Dynam. Sys. 4 (1984), 499–507.Google Scholar
Bergelson, V. and Simmons, D.. New examples of complete sets, with connection to a Diophantine theorem of Furstenberg. Acta Arith. 177(2) (2017), 101–131.Google Scholar
Boshernitzan, M. D.. Elementary proof of Furstenberg’s diophantine result. Proc. Amer. Math. Soc. 122(1) (1994), 67–70.Google Scholar
Boshernitzan, M. D.. Uniform distribution and Hardy fields. J. Anal. Math. 62 (1994), 225–240.Google Scholar
Furstenberg, H.. Disjointness in ergodic theory, minimal sets, and a problem in diophantine approximation. Math. Syst. Theory 1 (1967), 1–49.Google Scholar
Gorodnik, A. and Kadyrov, S.. Algebraic numbers, hyperbolicity, and density modulo 1. J. Number Theory 132 (2012), 2499–2509.Google Scholar
Hardy, G. H. and Littlewood, J. E.. Some problems of diophantine approximation, I. The fractional part of n k𝛩. Acta Math. 37 (1914), 155–191.Google Scholar
Kra, B.. A generalization of Furstenberg’s diophantine theorem. Proc. Amer. Math. Soc. 127(7) (1999), 1951–1956.Google Scholar
Meiri, D.. Entropy and uniform distribution of orbits in 𝕋d. Israel J. Math. 105 (1998), 155–183.Google Scholar
Muchnik, R.. Semigroup actions on 𝕋n. Geom. Dedicata 110 (2005), 1–47.Google Scholar
Urban, R.. Algebraic numbers and density modulo 1. J. Number Theory 128(3) (2008), 645–661.Google Scholar
Urban, R.. On density modulo 1 of some expressions containing algebraic integers. Acta Arith. 127(3) (2007), 217–229.Google Scholar
Urban, R.. Multiplicatively independent integers and dense modulo 1 sets of sums. Unif. Distrib. Theory 4 (2009), 27–33.Google Scholar