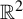Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Frantzikinakis, Nikos
2023.
Joint ergodicity of sequences.
Advances in Mathematics,
Vol. 417,
Issue. ,
p.
108918.
Chen, Xuezhi
and
Guo, Jingwei
2024.
A polynomial Roth theorem for corners in $${\mathbb {R}}^2$$ and a related bilinear singular integral operator.
Mathematische Annalen,
Vol. 390,
Issue. 1,
p.
255.