No CrossRef data available.
Published online by Cambridge University Press: 31 August 2022
We consider graphs consisting of finitely many internal rays for degenerating Newton maps and state a convergence result. As an application, we prove that a hyperbolic component in the moduli space of quartic Newton maps is bounded if and only if every element has degree 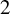 $2$ on the immediate basin of each root. This provides the first complete description of bounded hyperbolic components in a complex two-dimensional moduli space.
$2$ on the immediate basin of each root. This provides the first complete description of bounded hyperbolic components in a complex two-dimensional moduli space.