Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T03:16:51.876Z Has data issue: false hasContentIssue false
  • English
  • Français

Periodic unique beta-expansions: the Sharkovskiĭ ordering

Published online by Cambridge University Press:  01 August 2009

JEAN-PAUL ALLOUCHE ,
MATTHEW CLARKE  and
NIKITA SIDOROV
JEAN-PAUL ALLOUCHE
Affiliation:
CNRS, LRI, UMR 8623, Université Paris-Sud, Bâtiment 490, F-91405 Orsay Cedex, France (email: [email protected])
MATTHEW CLARKE
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, Cambridge, CB3 0WB, UK (email: [email protected])
NIKITA SIDOROV
Affiliation:
School of Mathematics, The University of Manchester, Oxford Road, Manchester M13 9PL, UK (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let β∈(1,2). Each x∈[0,1/(β−1)] can be represented in the form where εk∈{0,1} for all k (a β-expansion of x). If 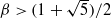, then, as is well known, there always exist x∈(0,1/(β−1)) which have a unique β-expansion. We study (purely) periodic unique β-expansions and show that for each n≥2 there exists 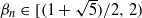such that there are no unique periodic β-expansions of smallest period n for β≤βn and at least one such expansion for β>βn. Furthermore, we prove that βk<βm if and only if k is less than m in the sense of the Sharkovskiĭ ordering. We give two proofs of this result, one of which is independent, and the other one links it to the dynamics of a family of trapezoidal maps.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 29 , Issue 4 , August 2009 , pp. 1055 - 1074
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Allouche, J.-P.. Théorie des Nombres et Automates, Thèse d’État, Université Bordeaux I, (1983). Available at: http://tel.archives-ouvertes.fr/tel-00343206/fr/ .Google Scholar
[2]Allouche, J.-P. and Cosnard, M.. Une propriété extrémale de la suite de Thue–Morse en rapport avec les cascades de Feigenbaum. Sém. Théorie des Nombres Bordeaux (1981/1982), 26-01–26-17.Google Scholar
[3]Allouche, J.-P. and Cosnard, M.. Itérations de fonctions unimodales et suites engendrées par automates. C. R. Acad. Sci. Paris, Série I 296 (1983), 159–162.Google Scholar
[4]Allouche, J.-P. and Cosnard, M.. The Komornik–Loreti constant is transcendental. Amer. Math. Monthly 107 (2000), 448–449.Google Scholar
[5]Allouche, J.-P. and Cosnard, M.. Non-integer bases, iteration of continuous real maps, and an arithmetic self-similar set. Acta Math. Hung. 91 (2001), 325–332.Google Scholar
[6]Allouche, J.-P. and Shallit, J.. The ubiquitous Prouhet–Thue–Morse sequence. Sequences and Their Applications: Proceedings of SETA ’98. Eds. C. Ding., T. Helleseth and H. Niederreiter. Springer, Berlin, 1999, pp. 1–16.Google Scholar
[7]Bruin, H.. Invariant measures of interval maps. PhD Thesis, Delft, 1994.Google Scholar
[8]Cosnard, M.. Étude de la classification topologique des fonctions unimodales. Ann. Inst. Fourier 35 (1985), 59–77.Google Scholar
[9]Daróczy, Z. and Katai, I.. Univoque sequences. Publ. Math. Debrecen 42 (1993), 397–407.Google Scholar
[10]Daróczy, Z. and Kátai, I.. On the structure of univoque numbers. Publ. Math. Debrecen 46 (1995), 385–408.Google Scholar
[11]Devaney, R.. An Introduction to Chaotic Dynamical Systems. Addison-Wesley, Reading, MA, 1989.Google Scholar
[12]Erdős, P., Joó, I. and Komornik, V.. Characterization of the unique expansions 1=∑ i=1∞q −n i and related problems. Bull. Soc. Math. France 118 (1990), 377–390.CrossRefGoogle Scholar
[13]Glendinning, P. and Sidorov, N.. Unique representations of real numbers in non-integer bases. Math. Res. Lett. 8 (2001), 535–543.Google Scholar
[14]Komornik, V. and Loreti, P.. Unique developments in non-integer bases. Amer. Math. Monthly 105 (1998), 636–639.Google Scholar
[15]Komornik, V. and de Vries, M.. Unique expansions of real numbers. Adv. Math. to appear. Preprint, 2007. Available at http://arxiv.org/abs/math/0609708v4.Google Scholar
[16]Louck, J. D. and Metropolis, N.. Symbolic Dynamics of Trapezoidal Maps (Mathematics and its Applications, 27). D. Reidel, Dordrecht, 1986.Google Scholar
[17]Lyndon, R. C. and Schützenberger, M. P.. The equation a M=b Nc P in a free group. Michigan Math. J. 9 (1962), 289–298.Google Scholar
[18]Milnor, J. and Thurston, W.. On iterated maps of the interval. Dynamical Systems (College Park, MD, 1986–1987) (Lecture Notes in Mathematics, 1342). Springer, Berlin, 1988, pp. 465–563.Google Scholar
[19]Parry, W.. On the β-expansions of real numbers. Acta Math. Acad. Sci. Hung. 11 (1960), 401–416.Google Scholar
[20]Sharkovskiĭ, O. M.. Co-existence of cycles of a continuous mapping of a line onto itself. Ukranian Math. Z. 16 (1964), 61–71.Google Scholar
[21]Sidorov, N.. Almost every number has a continuum of β-expansions. Amer. Math. Monthly 110 (2003), 838–842.Google Scholar
[22]Sidorov, N.. Combinatorics of linear iterated function systems with overlaps. Nonlinearity 20 (2007), 1299–1312.Google Scholar