Hostname: page-component-848d4c4894-v5vhk Total loading time: 0 Render date: 2024-07-03T06:50:40.115Z Has data issue: false hasContentIssue false
  • English
  • Français

Periodic points of post-critically algebraic holomorphic endomorphisms

Part of: Complex dynamical systems Holomorphic mappings and correspondences

Published online by Cambridge University Press:  11 May 2021

VAN TU LE Open the ORCID record for VAN TU LE [Opens in a new window]
VAN TU LE*
Affiliation:
Institut de Mathématiques de Toulouse, UMR5219, Université de Toulouse, CNRS, UPS IMT, 118 route de Narbonne, F-31062 Toulouse Cedex 9, France (e-mail: [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A holomorphic endomorphism of 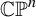${{\mathbb {CP}}}^n$ is post-critically algebraic if its critical hypersurfaces are periodic or preperiodic. This notion generalizes the notion of post-critically finite rational maps in dimension one. We will study the eigenvalues of the differential of such a map along a periodic cycle. When 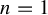$n=1$ , a well-known fact is that the eigenvalue along a periodic cycle of a post-critically finite rational map is either superattracting or repelling. We prove that, when 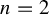$n=2$ , the eigenvalues are still either superattracting or repelling. This is an improvement of a result by Mattias Jonsson [Some properties of 2-critically finite holomorphic maps of P2. Ergod. Th. & Dynam. Sys.18(1) (1998), 171–187]. When $n\geq 2$ and the cycle is outside the post-critical set, we prove that the eigenvalues are repelling. This result improves one obtained by Fornæss and Sibony [Complex dynamics in higher dimension. II. Modern Methods in Complex Analysis (Princeton, NJ, 1992) (Annals of Mathematics Studies, 137). Ed. T. Bloom, D. W. Catlin, J. P. D’Angelo and Y.-T. Siu, Princeton University Press, 1995, pp. 135–182] under a hyperbolicity assumption on the complement of the post-critical set.

Keywords

holomorphic dynamicsperiodic pointseigenvaluespost-critically finitepost-critically algebraic

MSC classification

Primary: 32H50: Iteration problems
Secondary: 37F99: None of the above, but in this section
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 7 , July 2022 , pp. 2382 - 2414
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abate, M.. Iteration Theory of Holomorphic Maps on Taut Manifolds. Mediterranean Press, Commenda di Rende, Italy, 1989.Google Scholar
Andreian Cazacu, C.. Coverings and convergence theorems. Progress in Analysis. Vol. I, II. Proc. 3rd Int. Congress of the International Society for Analysis, its Applications and Computation (ISAAC) (Berlin, Germany, 20–25 August, 2001). World Scientific, River Edge, NJ, 2003, pp. 169–175.Google Scholar
Astorg, M.. Dynamics of post-critically finite maps in higher dimension. Ergod. Th. & Dynam. Sys. 40(2) (2020), 289–308.CrossRefGoogle Scholar
Cartan, H.. Sur les rétractions d’une variété. C. R. Math. Acad. Sci. Paris 303 (1986), 715–716.Google Scholar
Chirka, E. M.. Complex Analytic Sets. Springer Science & Business Media, Kluwer Academic, Dordrecht, 1989. Translated from the Russian by R. A. M. Hoksbergen.CrossRefGoogle Scholar
Dinh, T.-C. and Sibony, N.. Dynamics in several complex variables: endomorphisms of projective spaces and polynomial-like mappings. Holomorphic Dynamical Systems: Lectures Given at the C.I.M.E. Summer School Held in Cetraro, Italy, 7–12 July, 2008. Springer, Berlin, 2010.Google Scholar
Fornæss, J. E. and Sibony, N.. Critically finite rational maps on ℙ2 . The Madison Symposium on Complex Analysis (University of Wisconsin-Madison, Madison, WI, USA, 2–7 June 1991) (Contemporary Mathematics, 137). American Mathematical Society, Providence, RI, 1992, pp. 245–260.CrossRefGoogle Scholar
Fornæss, J. E. and Sibony, N.. Complex dynamics in higher dimension. I. Astérisque 222 (1994), 201–231.Google Scholar
Fornaess, J. E. and Sibony, N.. Complex dynamics in higher dimension. II. Modern Methods in Complex Analysis (Princeton, NJ, 1992) (Annals of Mathematics Studies, 137). Ed. Bloom, T., Catlin, D. W., D'Angelo, J. P. and Siu, Y.-T., Princeton University Press, 1995, pp. 135–182.Google Scholar
Gauthier, T., Hutz, B. and Kaschner, S.. Symmetrization of rational maps: arithmetic properties and families of Lattès maps of ℙ k . Preprint, 2018, arXiv:1603.04887.Google Scholar
Grauert, H. and Remmert, R.. Komplexe räume. Math. Ann. 136(3) (1958), 245–318.CrossRefGoogle Scholar
Gunning, R. C.. Introduction to Holomorphic Functions of Several Variables. Vols. 1–3. Wadsworth & Brooks/Cole Advanced Books & Software, Florence, KY, 1990.Google Scholar
Gauthier, T. and Vigny, G.. The geometric dynamical Northcott and Bogomolov properties. Preprint, 2020, arXiv:1912.07907.Google Scholar
Hubbard, J. H. and Papadopol, P.. Superattractive fixed points in ℂ n . Indiana Univ. Math. J. 43(1) (1994), 321–365.CrossRefGoogle Scholar
Ji, Z.. Structure of Julia sets for post-critically finite endomorphisms on ℙ2. Preprint, 2020, arXiv:2010.11094.CrossRefGoogle Scholar
Jonsson, M.. Some properties of 2-critically finite holomorphic maps of ℙ2 . Ergod. Th. & Dynam. Sys. 18(1) (1998), 171–187.CrossRefGoogle Scholar
Milnor, J.. Singular Points of Complex Hypersurfaces (Annals of Mathematics Studies, 61). Princeton University Press, Princeton, NJ, 1968.Google Scholar
Milnor, J.. Dynamics in One Complex Variable (Annals of Mathematics Studies, 160), 3rd edn. Princeton University Press, Princeton, NJ, 2011.Google Scholar
Ingram, P., Ramadas, R. and Silverman, J. H.. Post-critically finite maps on ${\mathbb{P}}^n$ for $n\ge 2$ are sparse. Preprint, 2019, arXiv:1910.11290.Google Scholar
Rong, F.. The Fatou set for critically finite maps. Proc. Amer. Math. Soc. 136(10) (2008), 3621–3625.CrossRefGoogle Scholar
Reid, M. and Shafarevich, I. R.. Basic Algebraic Geometry 1. Springer, Berlin, 2013.Google Scholar
Seade, J.. On the Topology of Isolated Singularities in Analytic Spaces (Progress in Mathematics, 241). Birkhäuser, Basel, 2006.Google Scholar
Seade, J.. On Milnor’s fibration theorem and its offspring after 50 years. Bull. Amer. Math. Soc. 56(2) (2019), 281–348.CrossRefGoogle Scholar
Sibony, N.. Dynamique des applications rationnelles de ℙk . Panor. Synthèses 8 (1999), 97–185.Google Scholar
Ueda, T.. Critical orbits of holomorphic maps on projective spaces. J. Geom. Anal. 8(2) (1998), 319.Google Scholar
Wall, C. T. C.. Singular Points of Plane Curves (London Mathematical Society Student Texts, 63). Cambridge University Press, Cambridge, 2004.CrossRefGoogle Scholar
Zariski, O.. Le problème des modules pour les branches planes: cours donné au Centre de Mathématiques de l’École Polytechnique. Centre de Mathématiques de l’École Polytechnique, Paris, 1973.Google Scholar