Article contents
Partitions by congruent sets and optimal positions
Published online by Cambridge University Press: 16 June 2010
Abstract
Let X be a metrizable space with a continuous group or semi-group action G. Let D be a non-empty subset of X. Our problem is how to choose a fixed number of sets in {g−1D; g∈G}, say σ−1D with σ∈τ, to maximize the cardinality of the partition ℙ({σ−1D; σ∈τ}) generated by them. Let 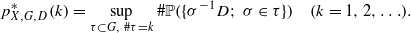 An infinite subset Σ of G is called an optimal position of the triple (X,G,D) if
An infinite subset Σ of G is called an optimal position of the triple (X,G,D) if 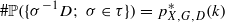 holds for any k=1,2,… and τ⊂Σ with #τ=k. In this paper, we discuss examples of the triple (X,G,D) admitting or not admitting an optimal position. Let X=G=ℝn (n≥1) , where the action g∈G to x∈X is the translation x−g. If D is the n-dimensional unit ball, then
holds for any k=1,2,… and τ⊂Σ with #τ=k. In this paper, we discuss examples of the triple (X,G,D) admitting or not admitting an optimal position. Let X=G=ℝn (n≥1) , where the action g∈G to x∈X is the translation x−g. If D is the n-dimensional unit ball, then 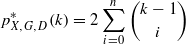 holds and the triple (X,G,D) admits an optimal position. In fact, if n≥2 and Σ is an infinite subset of G such that for some δ with 0<δ<1 , Σ⊂{x∈ℝn ; ‖x‖=δ}, and that any subset of Σ with cardinality n+1 is not on a hyperplane, then Σ is an optimal position of the triple (X,G,D) . We have determined the primitive factor of the uniform sets coming from these optimal positions. We also show that in the above setting with n=2 and the unit square D′ in place of the unit disk D, the maximal pattern complexity is unchanged and p*X,G,D′(k)=k2 −k+2 , but there is no optimal position.
holds and the triple (X,G,D) admits an optimal position. In fact, if n≥2 and Σ is an infinite subset of G such that for some δ with 0<δ<1 , Σ⊂{x∈ℝn ; ‖x‖=δ}, and that any subset of Σ with cardinality n+1 is not on a hyperplane, then Σ is an optimal position of the triple (X,G,D) . We have determined the primitive factor of the uniform sets coming from these optimal positions. We also show that in the above setting with n=2 and the unit square D′ in place of the unit disk D, the maximal pattern complexity is unchanged and p*X,G,D′(k)=k2 −k+2 , but there is no optimal position.
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 2010
References
- 3
- Cited by


