Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T12:47:11.793Z Has data issue: false hasContentIssue false
  • English
  • Français

Parameter rigid actions of the Heisenberg groups

Published online by Cambridge University Press:  01 December 2007

NATHAN M. DOS SANTOS
NATHAN M. DOS SANTOS*
Affiliation:
Instituto de Matemática, Universidade Federal Fluminense, 24020-005, Niterói, RJ, Brazil (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

A locally free action of a Lie group is parameter rigid if for each other action with the same orbit foliation there exists a 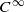orbit-preserving diffeomorphism which conjugates the action to a reparametrization of the other by an automorphism of the Lie group. We show that for actions of the Heisenberg groups, if the first leafwise cohomology group of the orbit foliation is isomorphic to the first cohomology of the Lie algebra of the group, then the action is parameter rigid. Using this, we give examples of parameter rigid actions for all of the Heisenberg groups.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 27 , Issue 6 , December 2007 , pp. 1719 - 1735
Copyright
Copyright © Cambridge University Press 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Arraut, J. L. and dos Santos, N. M.. The characteristic mapping of a foliated bundle. Topology 31 (1992), 545–555.CrossRefGoogle Scholar
[2]Atiyah, M. F. and Wall, C. T. C.. Cohomology of groups. Algebraic Number Theory. Eds. J. W. S. Cassels and A. Fröhlich. Academic Press, New York, 1967, pp. 95–117.Google Scholar
[3]Brezin, J.. Harmonic Analysis on Compact Solvmanifolds (Lecture Notes in Mathematics, 602). Springer, Berlin, 1977.CrossRefGoogle Scholar
[4]Corwin, L. and Greenleaf, F. P.. Representations of Nilpotent Lie Groups and their Applications. Part 1: Basic Theory and Examples. Cambridge University Press, Cambridge, 1990.Google Scholar
[5]Halperin, S., Werner, G. and Vanstone, R.. Connections, Curvature and Cohomology. Academic Press, New York, 1972.Google Scholar
[6]Jenkins, J. W.. Growth of connected localy compact groups. J. Funct. Anal. 12 (1973), 113–127.CrossRefGoogle Scholar
[7]Mañé, R.. Ergodic Theory and Differentiable Dynamics. Springer, New York, 1987.Google Scholar
[8]Matsumoto, S. and Mitsumatsu, Y.. Leafwise cohomology and rigidity of certain Lie group actions. Ergod. Th. & Dynam. Sys. 23 (2003), 1839–1866.Google Scholar
[9]Pereira, M. S. and dos Santos, N. M.. On the cohomology of foliated bundles. Proyecciones 21(2) (2002), 173–195.Google Scholar
[10]dos Santos, N. M.. Actions of Lie groups on closed manifolds. Ergod. Th. & Dynam. Sys. 22 (2002), 591–600.CrossRefGoogle Scholar