Consider the quadratic family 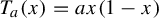$T_a(x) = a x (1 - x)$ for 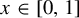$x \in [0, 1]$ and mixing Collet–Eckmann (CE) parameters 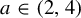$a \in (2,4)$. For bounded 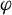$\varphi $, set $\tilde \varphi _{a} := \varphi - \int \varphi \, d\mu _a$, with 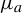$\mu _a$ the unique acim of 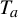$T_a$, and put 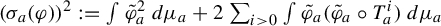$(\sigma _a (\varphi ))^2 := \int \tilde \varphi _{a}^2 \, d\mu _a + 2 \sum _{i>0} \int \tilde \varphi _{a} (\tilde \varphi _{a} \circ T^i_{a}) \, d\mu _a$. For any mixing Misiurewicz parameter 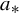$a_{*}$, we find a positive measure set $\Omega _{*}$ of mixing CE parameters, containing 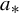$a_{*}$ as a Lebesgue density point, such that for any Hölder $\varphi $ with 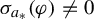$\sigma _{a_{*}}(\varphi )\ne 0$, there exists 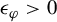$\epsilon _\varphi>0$ such that, for normalized Lebesgue measure on 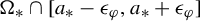$\Omega _{*}\cap [a_{*}-\epsilon _\varphi , a_{*}+\epsilon _\varphi ]$, the functions 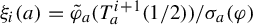$\xi _i(a)=\tilde \varphi _a(T_a^{i+1}(1/2))/\sigma _a (\varphi )$ satisfy an almost sure invariance principle (ASIP) for any error exponent 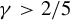$\gamma>2/5$. (In particular, the Birkhoff sums satisfy this ASIP.) Our argument goes along the lines of Schnellmann’s proof for piecewise expanding maps. We need to introduce a variant of Benedicks–Carleson parameter exclusion and to exploit fractional response and uniform exponential decay of correlations from Baladi et al [Whitney–Hölder continuity of the SRB measure for transversal families of smooth unimodal maps. Invent. Math. 201 (2015), 773–844].