Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Lomonaco, Luna
and
Petersen, Carsten Lunde
2017.
On quasi-conformal (in-) compatibility of satellite copies of the Mandelbrot set: I.
Inventiones mathematicae,
Vol. 210,
Issue. 2,
p.
615.
Lomonaco, Luna
Lunde Petersen, Carsten
and
Shen, Weixiao
2017.
On parabolic external maps.
Discrete & Continuous Dynamical Systems - A,
Vol. 37,
Issue. 10,
p.
5085.
Bullett, Shaun
Lomonaco, Luna
and
Siqueira, Carlos
2019.
New Trends in One-Dimensional Dynamics.
Vol. 285,
Issue. ,
p.
51.
Bullett, Shaun
and
Lomonaco, Luna
2020.
Mating quadratic maps with the modular group II.
Inventiones mathematicae,
Vol. 220,
Issue. 1,
p.
185.
Lee, Seung-Yeop
Lyubich, Mikhail
Makarov, Nikolai G.
and
Mukherjee, Sabyasachi
2021.
Schwarz reflections and anti-holomorphic correspondences.
Advances in Mathematics,
Vol. 385,
Issue. ,
p.
107766.
Blokh, Alexander
Oversteegen, Lex
and
Timorin, Vladlen
2022.
Cutpoints of Invariant Subcontinua of Polynomial Julia Sets.
Arnold Mathematical Journal,
Vol. 8,
Issue. 2,
p.
271.
Bullett, Shaun
and
Lomonaco, Luna
2022.
Dynamics of modular matings.
Advances in Mathematics,
Vol. 410,
Issue. ,
p.
108758.
Blokh, Alexander
Haïssinsky, Peter
Oversteegen, Lex
and
Timorin, Vladlen
2023.
On critical renormalization of complex polynomials.
Advances in Mathematics,
Vol. 428,
Issue. ,
p.
109135.
Lyubich, Mikhail
Mazor, Jacob
and
Mukherjee, Sabyasachi
2024.
Antiholomorphic correspondences and mating I: Realization theorems.
Communications of the American Mathematical Society,
Vol. 4,
Issue. 11,
p.
495.
Bullett, Shaun
and
Lomonaco, Luna
2024.
Mating quadratic maps with the modular group III: The modular Mandelbrot set.
Advances in Mathematics,
Vol. 458,
Issue. ,
p.
109956.
Zhang, Runze
2024.
On dynamical parameter space of cubic polynomials with a parabolic fixed point.
Journal of the London Mathematical Society,
Vol. 110,
Issue. 6,
MATUS DE LA PARRA, V.
2024.
Equidistribution for matings of quadratic maps with the modular group.
Ergodic Theory and Dynamical Systems,
Vol. 44,
Issue. 3,
p.
859.
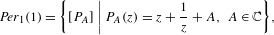 $$\begin{eqnarray}\mathit{Per}_{1}(1)=\left\{[P_{A}]\,\bigg|\,P_{A}(z)=z+\frac{1}{z}+A,~A\in \mathbb{C}\right\}\!,\end{eqnarray}$$
$$\begin{eqnarray}\mathit{Per}_{1}(1)=\left\{[P_{A}]\,\bigg|\,P_{A}(z)=z+\frac{1}{z}+A,~A\in \mathbb{C}\right\}\!,\end{eqnarray}$$

