Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T00:23:36.094Z Has data issue: false hasContentIssue false
  • English
  • Français

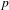$p$-adic Mahler measure and $\mathbb{Z}$-covers of links

Published online by Cambridge University Press:  29 June 2018

JUN UEKI
JUN UEKI*
Affiliation:
Department of Mathematics, School of System Design and Technology, Tokyo Denki University, 5 Senju Asahi-cho, Adachi-ku, Tokyo, 120-8551, Japan email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 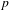$p$ be a prime number. We develop a theory of 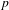$p$-adic Mahler measure of polynomials and apply it to the study of $\mathbb{Z}$-covers of rational homology 3-spheres branched over links. We obtain a 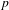$p$-adic analogue of the asymptotic formula of the torsion homology growth and a balance formula among the leading coefficient of the Alexander polynomial, the 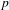$p$-adic entropy and the Iwasawa 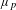$\unicode[STIX]{x1D707}_{p}$-invariant. We also apply the purely 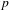$p$-adic theory of Besser–Deninger to $\mathbb{Z}$-covers of links. In addition, we study the entropies of profinite cyclic covers of links. We examine various examples throughout the paper.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 1 , January 2020 , pp. 272 - 288
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, R. L., Konheim, A. G. and McAndrew, M. H.. Topological entropy. Trans. Amer. Math. Soc. 114 (1965), 309–319.Google Scholar
Besser, A. and Deninger, C.. p-adic Mahler measures. J. Reine Angew. Math. 517 (1999), 19–50.10.1515/crll.1999.093Google Scholar
Bowen, R.. Entropy for group endomorphisms and homogeneous spaces. Trans. Amer. Math. Soc. 153 (1971), 401–414.10.1090/S0002-9947-1971-0274707-XGoogle Scholar
Boyd, D. W.. Mahler’s measure and invariants of hyperbolic manifolds. Number Theory for the Millennium, I (Urbana, IL, 2000). A K Peters, Natick, MA, 2002, pp. 127–143.Google Scholar
Boyd, D. W., Rodriguez-Villegas, F. and Dunfield, N.. Mahler’s measure and the dilogarithm (II). Preprint, 2003, arXiv:0308041v2.Google Scholar
Bergeron, N. and Venkatesh, A.. The asymptotic growth of torsion homology for arithmetic groups. J. Inst. Math. Jussieu 12(2) (2013), 391–447.Google Scholar
Deninger, C.. p-adic entropy and a p-adic Fuglede–Kadison determinant. Algebra, Arithmetic, and Geometry: in Honor of Yu. I. Manin. Vol. I (Progress in Mathematics, 269) . Birkhäuser Boston, Boston, MA, 2009, pp. 423–442.Google Scholar
Dikranjan, D. and Giordano Bruno, A.. The bridge theorem for totally disconnected LCA groups. Topology Appl. 169 (2014), 21–32.10.1016/j.topol.2014.02.029Google Scholar
Everest, G. and Ward, T.. Heights of Polynomials and Entropy in Algebraic Dynamics (Universitext) . Springer, London, 1999.Google Scholar
Fox, R. H.. Free differential calculus. III. Subgroups. Ann. of Math. (2) 64 (1956), 407–419.Google Scholar
González-Acuña, F. and Short, H.. Cyclic branched coverings of knots and homology spheres. Rev. Mat. Univ. Complut. Madrid 4(1) (1991), 97–120.Google Scholar
Giordano Bruno, A. and Virili, S.. Algebraic Yuzvinski formula. J. Algebra 423 (2015), 114–147.Google Scholar
Hillman, J.. Algebraic Invariants of Links (Series on Knots and Everything, 52) , 2nd edn. World Scientific, Hackensack, NJ, 2012.Google Scholar
Hillman, J., Matei, D. and Morishita, M.. Pro-p link groups and p-homology groups. Primes and Knots (Contemporary Mathematics, 416) . American Mathematical Society, Providence, RI, 2006, pp. 121–136.10.1090/conm/416/07890Google Scholar
Iwasawa, K.. On 𝛤-extensions of algebraic number fields. Bull. Amer. Math. Soc. (N.S.) 65 (1959), 183–226.Google Scholar
Kadokami, T. and Mizusawa, Y.. Iwasawa type formula for covers of a link in a rational homology sphere. J. Knot Theory Ramifications 17(10) (2008), 1199–1221.Google Scholar
Kadokami, T. and Mizusawa, Y.. On the Iwasawa invariants of a link in the 3-sphere. Kyushu J. Math. 67(1) (2013), 215–226.10.2206/kyushujm.67.215Google Scholar
Lalín, M. N.. Some examples of Mahler measures as multiple polylogarithms. J. Number Theory 103(1) (2003), 85–108.Google Scholar
Lalín, M. N.. Mahler measure and volumes in hyperbolic space. Geom. Dedicata 107 (2004), 211–234.10.1007/s10711-004-8123-8Google Scholar
Le, T.. Homology torsion growth and Mahler measure. Comment. Math. Helv. 89(3) (2014), 719–757.Google Scholar
Lind, D. A. and Ward, T.. Automorphisms of solenoids and p-adic entropy. Ergod. Th. & Dynam. Sys. 8(3) (1988), 411–419.10.1017/S0143385700004545Google Scholar
Mihara, T.. Singular homology of non-archimedean analytic spaces and integration along cycles. Preprint, 2012, arXiv:1211.1422v1.Google Scholar
Mayberry, J. P. and Murasugi, K.. Torsion-groups of abelian coverings of links. Trans. Amer. Math. Soc. 271(1) (1982), 143–173.Google Scholar
Noguchi, A.. Zeros of the Alexander polynomial of knot. Osaka J. Math. 44(3) (2007), 567–577.Google Scholar
Porti, J.. Mayberry–Murasugi’s formula for links in homology 3-spheres. Proc. Amer. Math. Soc. 132(11) (2004), 3423–3431 (electronic).Google Scholar
Riley, R.. Growth of order of homology of cyclic branched covers of knots. Bull. Lond. Math. Soc. 22(3) (1990), 287–297.Google Scholar
Rolfsen, D.. Knots and Links (Mathematics Lecture Series, 7) . Publish or Perish, Berkeley, CA, 1976.Google Scholar
Sakuma, M.. On the polynomials of periodic links. Math. Ann. 257(4) (1981), 487–494.Google Scholar
Shnirel’man(Schnirelmann), L. G.. Sur les fonctions dans les corps normés et algébriquement fermés. Izv. Akad. Nauk SSSR Ser. Mat. 2(5–6) (1938), 487–498 (Russian).Google Scholar
Smyth, C. J.. On measures of polynomials in several variables. Bull. Aust. Math. Soc. 23(1) (1981), 49–63.Google Scholar
Silver, D. S. and Williams, S. G.. Mahler measure, links and homology growth. Topology 41(5) (2002), 979–991.Google Scholar
Tange, R.. Fox formulas for twisted Alexander invariants associated to representations of knot groups over rings of $S$ -integers. Preprint, 2017, arXiv.Google Scholar
Ueki, J.. On the Iwasawa 𝜇-invariants of branched Z p-covers. Proc. Japan Acad. Ser. A Math. Sci. 92(6) (2016), 67–72.Google Scholar
Ueki, J.. On the Iwasawa invariants for links and Kida’s formula. Internat. J. Math. 28(6) (2017), 1750035, 30.10.1142/S0129167X17500355Google Scholar
Ueki, J.. The profinite completions of knot groups determine the Alexander polynomials. Algebr. Geom. Topol., to appear. Preprint, 2018, arXiv:1702.03836, 13 pages.Google Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79) . Springer, New York, 1982.10.1007/978-1-4612-5775-2Google Scholar
Washington, L. C.. Introduction to Cyclotomic Fields (Graduate Texts in Mathematics, 83) , 2nd edn. Springer, New York, 1997.Google Scholar
Weber, C.. Sur une formule de R. H. Fox concernant l’homologie des revêtements cycliques. Enseign. Math. (2) 25(3–4) (1980), 261–272.Google Scholar