Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T01:11:06.190Z Has data issue: false hasContentIssue false
  • English
  • Français

Orbital shadowing, internal chain transitivity and $\unicode[STIX]{x1D714}$-limit sets

Published online by Cambridge University Press:  13 July 2016

CHRIS GOOD  and
JONATHAN MEDDAUGH
CHRIS GOOD
Affiliation:
University of Birmingham, School of Mathematics, Birmingham B15 2TT, UK email [email protected], [email protected]
JONATHAN MEDDAUGH
Affiliation:
University of Birmingham, School of Mathematics, Birmingham B15 2TT, UK email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

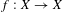Let $f:X\rightarrow X$ be a continuous map on a compact metric space, let 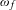$\unicode[STIX]{x1D714}_{f}$ be the collection of $\unicode[STIX]{x1D714}$-limit sets of 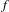$f$ and let 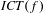$\mathit{ICT}(f)$ be the collection of closed internally chain transitive subsets. Provided that 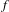$f$ has shadowing, it is known that the closure of 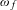$\unicode[STIX]{x1D714}_{f}$ in the Hausdorff metric coincides with 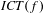$\mathit{ICT}(f)$. In this paper, we prove that 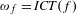$\unicode[STIX]{x1D714}_{f}=\mathit{ICT}(f)$ if and only if 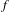$f$ satisfies Pilyugin’s notion of orbital limit shadowing. We also characterize those maps for which 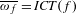$\overline{\unicode[STIX]{x1D714}_{f}}=\mathit{ICT}(f)$ in terms of a variation of orbital shadowing.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 1 , February 2018 , pp. 143 - 154
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barwell, A. D.. A characterization of 𝜔-limit sets of piecewise monotone maps of the interval. Fund. Math. 207(2) (2010), 161–174.Google Scholar
Barwell, A. D., Good, C., Knight, R. and Raines, B. E.. A characterization of 𝜔-limit sets in shift spaces. Ergod. Th. & Dynam. Sys. 30(1) (2010), 21–31.CrossRefGoogle Scholar
Barwell, A. D., Good, C., Oprocha, P. and Raines, B. E.. Characterizations of 𝜔-limit sets of topologically hyperbolic spaces. Discrete Contin. Dyn. Syst. 33(5) (2013), 1819–1833.Google Scholar
Barwell, A. D., Meddaugh, J. and Raines, B. E.. Shadowing and 𝜔-limit sets of circular Julia sets. Ergod. Th. & Dynam. Sys. 35(4) (2015), 1045–1055.Google Scholar
Barwell, A. D. and Raines, B. E.. The 𝜔-limit sets of quadratic Julia sets. Ergod. Th. & Dynam. Sys. 35(2) (2015), 337–358.Google Scholar
Blokh, A., Bruckner, A. M., Humke, P. D. and Smítal, J.. The space of 𝜔-limit sets of a continuous map of the interval. Trans. Amer. Math. Soc. 348(4) (1996), 1357–1372.Google Scholar
Bowen, R.. 𝜔-limit sets for axiom A diffeomorphisms. J. Differential Equations 18(2) (1975), 333–339.Google Scholar
Brian, W. R., Meddaugh, J. and Raines, B. E.. Chain transitivity and variations of the shadowing property. Ergod. Th. & Dynam. Sys. 35(7) (2015), 2044–2052.Google Scholar
Coven, E. M., Kan, I. and Yorke, J. A.. Pseudo-orbit shadowing in the family of tent maps. Trans. Amer. Math. Soc. 308(1) (1988), 227–241.Google Scholar
Fakhari, A. and Ghane, F. H.. On shadowing: ordinary and ergodic. J. Math. Anal. Appl. 364(1) (2010), 151–155.Google Scholar
Hirsch, M. W., Smith, H. L. and Zhao, X.-Q.. Chain transitivity, attractivity, and strong repellors for semidynamical systems. J. Dynam. Differential Equations 13(1) (2001), 107–131.CrossRefGoogle Scholar
Kočan, Z., Kornecká-Kurková, V. and Málek, M.. On the centre and the set of 𝜔-limit points of continuous maps on dendrites. Topology Appl. 156(18) (2009), 2923–2931.Google Scholar
López, V. J. and Smítal, J.. 𝜔-limit sets for triangular mappings. Fund. Math. 167(1) (2001), 1–15.Google Scholar
Mai, J.-H. and Shao, S.. Spaces of 𝜔-limit sets of graph maps. Fund. Math. 196(1) (2007), 91–100.CrossRefGoogle Scholar
Meddaugh, J. and Raines, B. E.. Shadowing and internal chain transitivity. Fund. Math. 222 (2013), 279–287.Google Scholar
Oprocha, P.. Shadowing, thick sets and the ramsey property. Ergod. Th. & Dynam. Sys. doi:10.1017/etds.2014.130, 14 pages. Published online: 9 January 2015.Google Scholar
Pilyugin, S. Yu.. Sets of dynamical systems with various limit shadowing properties. J. Dynam. Differential Equations 19(3) (2007), 747–775.CrossRefGoogle Scholar
Pilyugin, S. Yu., Rodionova, A. A. and Sakai, K.. Orbital and weak shadowing properties. Discrete Contin. Dyn. Syst. 9(2) (2003), 287–308.CrossRefGoogle Scholar
Pokluda, D.. Characterization of 𝜔-limit sets of continuous maps of the circle. Comment. Math. Univ. Carolin. 43(3) (2002), 575–581.Google Scholar
Puljiz, M.. Shadowing and $\unicode[STIX]{x1D714}$ -limit sets. Private communication, 2013.Google Scholar