Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dani, S. G.
and
Smillie, John
1984.
Uniform distribution of horocycle orbits for Fuchsian
groups.
Duke Mathematical Journal,
Vol. 51,
Issue. 1,
Margulis, G. A.
1988.
Algebra Some Current Trends.
Vol. 1352,
Issue. ,
p.
130.
MARGULIS, G.A.
1989.
Number Theory, Trace Formulas and Discrete Groups.
p.
377.
Dani, S. G.
and
Margulis, G. A.
1989.
Values of quadratic forms at primitive integral points.
Inventiones Mathematicae,
Vol. 98,
Issue. 2,
p.
405.
Dani, S. G.
1995.
Proceedings of the International Congress of Mathematicians.
p.
780.
Safonov, A. V.
Starkov, A. N.
and
Stepin, A. M.
1995.
Dynamical Systems IX.
Vol. 66,
Issue. ,
p.
177.
Старков, Александр Николаевич
and
Starkov, Aleksandr Nikolaevich
1997.
Новый прогресс в теории однородных потоков.
Успехи математических наук,
Vol. 52,
Issue. 4,
p.
87.
Ledrappier, François
1999.
Distribution des orbites des réseaux sur le plan réel.
Comptes Rendus de l'Académie des Sciences - Series I - Mathematics,
Vol. 329,
Issue. 1,
p.
61.
Nogueira, Arnaldo
2002.
Orbit distribution on R2 under the natural action of SL(2,Z).
Indagationes Mathematicae,
Vol. 13,
Issue. 1,
p.
103.
Kleinbock, Dmitry
Shah, Nimish
and
Starkov, Alexander
2002.
Vol. 1,
Issue. ,
p.
813.
Kuessner, Thilo
2003.
Efficient fundamental cycles of cusped hyperbolic manifolds.
Pacific Journal of Mathematics,
Vol. 211,
Issue. 2,
p.
283.
NOGUEIRA, ARNALDO
2010.
Lattice orbit distribution on ℝ2.
Ergodic Theory and Dynamical Systems,
Vol. 30,
Issue. 4,
p.
1201.
GUILLOUX, ANTONIN
2010.
POLYNOMIAL DYNAMIC AND LATTICE ORBITS IN S-ARITHMETIC HOMOGENEOUS SPACES.
Confluentes Mathematici,
Vol. 02,
Issue. 01,
p.
1.
Bourgain, J.
Sarnak, P.
and
Ziegler, T.
2013.
From Fourier Analysis and Number Theory to Radon Transforms and Geometry.
Vol. 28,
Issue. ,
p.
67.
Strömbergsson, Andreas
2013.
On the deviation of ergodic averages for horocycle flows.
Journal of Modern Dynamics,
Vol. 7,
Issue. 2,
p.
291.
Lindenstrauss, Elon
and
Margulis, Gregory
2014.
Effective estimates on indefinite ternary forms.
Israel Journal of Mathematics,
Vol. 203,
Issue. 1,
p.
445.
Athreya, Jayadev S.
and
Cheung, Yitwah
2014.
A Poincaré Section for the Horocycle Flow on the Space of Lattices.
International Mathematics Research Notices,
Vol. 2014,
Issue. 10,
p.
2643.
Strömbergsson, Andreas
2015.
An effective Ratner equidistribution result for SL(2,R)⋉R2.
Duke Mathematical Journal,
Vol. 164,
Issue. 5,
Sarnak, Peter
and
Ubis, Adrián
2015.
The horocycle flow at prime times.
Journal de Mathématiques Pures et Appliquées,
Vol. 103,
Issue. 2,
p.
575.
Peckner, Ryan
2018.
Möbius disjointness for homogeneous dynamics.
Duke Mathematical Journal,
Vol. 167,
Issue. 14,


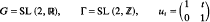
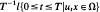 converges to μ(Ω).
converges to μ(Ω).