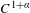Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Alves, José F
and
Khan, Muhammad Ali
2019.
Statistical instability for contracting Lorenz flows.
Nonlinearity,
Vol. 32,
Issue. 11,
p.
4413.
Liao, Gang
2019.
Regularity of SRB Entropy for Geometric Lorenz Attractors.
Journal of Statistical Physics,
Vol. 174,
Issue. 3,
p.
536.
Bahsoun, Wael
Melbourne, Ian
and
Ruziboev, Marks
2020.
Variance Continuity for Lorenz Flows.
Annales Henri Poincaré,
Vol. 21,
Issue. 6,
p.
1873.
Gianfelice, Michele
and
Vaienti, Sandro
2020.
Stochastic Stability of the Classical Lorenz Flow Under Impulsive Type Forcing.
Journal of Statistical Physics,
Vol. 181,
Issue. 1,
p.
163.
ARAUJO, VITOR
2021.
Finitely many physical measures for sectional-hyperbolic attracting sets and statistical stability.
Ergodic Theory and Dynamical Systems,
Vol. 41,
Issue. 9,
p.
2706.
Larkin, Andrew
2023.
Quenched Decay of Correlations for One-dimensional Random Lorenz Maps.
Journal of Dynamical and Control Systems,
Vol. 29,
Issue. 1,
p.
185.
Gianfelice, Michele
2023.
Stochastic and statistical stability of the classical Lorenz flow under perturbations modeling anthropogenic type forcing.
Bollettino dell'Unione Matematica Italiana,
Vol. 16,
Issue. 2,
p.
363.
Bahsoun, Wael
and
Galatolo, Stefano
2024.
Linear response due to singularities.
Nonlinearity,
Vol. 37,
Issue. 7,
p.
075010.
Fanaee, Mohammad
and
Soufi, Mohammad
2025.
Singular hyperbolic attractors are statistical stable.
São Paulo Journal of Mathematical Sciences,
Vol. 19,
Issue. 1,
ALVES, JOSÉ F.
and
ETUBI, ODAUDU
2025.
Modulus of continuity of invariant densities and entropies for piecewise expanding maps.
Ergodic Theory and Dynamical Systems,
p.
1.