Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-24T17:20:51.789Z Has data issue: false hasContentIssue false
  • English
  • Français

On the rotation sets of generic homeomorphisms on the torus 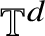${\mathbb T^d}$

Part of: Low-dimensional dynamical systems Topological dynamics Smooth dynamical systems: general theory

Published online by Cambridge University Press:  07 October 2020

HEIDES LIMA  and
PAULO VARANDAS
HEIDES LIMA
Affiliation:
Universidade Federal da Bahia, Av. Ademar de Barros s/n, Salvador, 40170-110, Brazil (e-mail: [email protected])
PAULO VARANDAS
Affiliation:
Departamento de Matemática e Estatística, Universidade Federal da Bahia, Av. Ademar de Barros s/n, Salvador, 40170-110, Brazil (e-mail: [email protected],[email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the rotation sets for homeomorphisms homotopic to the identity on the torus 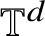$\mathbb T^d$ , 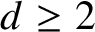$d\ge 2$ . In the conservative setting, we prove that there exists a Baire residual subset of the set 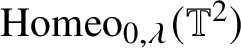$\text {Homeo}_{0, \lambda }(\mathbb T^2)$ of conservative homeomorphisms homotopic to the identity so that the set of points with wild pointwise rotation set is a Baire residual subset in 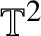$\mathbb T^2$ , and that it carries full topological pressure and full metric mean dimension. 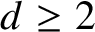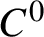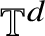Moreover, we prove that for every $d\ge 2$ the rotation set of $C^0$ -generic conservative homeomorphisms on $\mathbb T^d$ is convex. Related results are obtained in the case of dissipative homeomorphisms on tori. The previous results rely on the description of the topological complexity of the set of points with wild historic behavior and on the denseness of periodic measures for continuous maps with the gluing orbit property.

Keywords

rotation setshomeomorphisms on torihistoric behaviortopological entropymetric mean dimensiongluing orbit propertyspecification

MSC classification

Primary: 37E45: Rotation numbers and vectors 37B40: Topological entropy 37C50: Approximate trajectories (pseudotrajectories, shadowing, etc.)
Secondary: 37E30: Homeomorphisms and diffeomorphisms of planes and surfaces
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 10 , October 2021 , pp. 2983 - 3022
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Addas-Zanata, S.. Area-preserving diffeomorphisms of the torus whose rotation sets have non-empty interior. Ergod. Th. & Dynam. Sys. 35(1) (2015), 1–33.CrossRefGoogle Scholar
Akin, E., Hurley, M. and Kennedy, J.. Dynamics of topologically generic homeomorphisms. Mem. Amer. Math. Soc. 783 (2003), viii+130pp.Google Scholar
Barreira, L., Li, J. and Valls, C.. Irregular sets are residual. Tohoku Math. J. 66 (2014), 471–489.10.2748/tmj/1432229192CrossRefGoogle Scholar
Barreira, L. and Saussol, B.. Variational principles and mixed multifractal spectra. Trans. Amer. Math. Soc. 353(10) (2001), 3919–3944.CrossRefGoogle Scholar
Barreira, L. and Schmeling, J.. Sets of ‘non–typical’ points have full topological entropy and full Hausdorff dimension. Israel J. Math. 116 (2000), 29–70.10.1007/BF02773211CrossRefGoogle Scholar
Bessa, M., Torres, M. J. and Varandas, P.. On the periodic orbits, shadowing and strong transitivity of continuous flows. Nonlinear Anal. 175 (2018), 191–209.CrossRefGoogle Scholar
Bomfim, T., Torres, M. J. and Varandas, P.. Topological features of flows with the reparametrized gluing orbit property. J. Differential Equations 262 (2017), 4292–4313.CrossRefGoogle Scholar
Bomfim, T., Torres, M. J. and Varandas, P.. Partial hyperbolicity and gluing orbit property. J. Diff. Equations, to appear.Google Scholar
Bomfim, T. and Varandas, P.. The gluing orbit property, uniform hyperbolicity and large deviation principles for semiflows. J. Differential Equations 267 (2019), 228–266.CrossRefGoogle Scholar
Bonomo, W., Lima, H. and Varandas, P.. The rotation sets of most volume preserving homeomorphisms on $\mathbb T^d$ are stable, convex and rational polyhedrons. Israel J. Math. to appear.Google Scholar
Bowen, R.. Entropy for group endomorphisms and homogeneous spaces. Trans. Amer. Math. Soc. 153 (1971), 401–414.CrossRefGoogle Scholar
Chen, E., Küpper, T. and Lin, S.. Topological entropy for divergence points. Ergod. Th. & Dynam. Sys. 25(4) (2005), 1173–1208.Google Scholar
Coven, E. M., Madden, J. and Nitecki, Z.. A note on generic properties of continuous maps. Ergod. Th. & Dynam. Sys. 2(21) (1982), 97–101.Google Scholar
de Melo, W. and van Strien, S.. One-dimensional Dynamics. (Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)]) Vol. 25. Springer, Berlin, 1993.Google Scholar
Denker, M., Grillenberger, C. and Sigmund, K.. Ergodic Theory on Compact Spaces. Springer, Berlin, 1976.CrossRefGoogle Scholar
Dong, Y., Oprocha, P. and Tian, X.. On the irregular points for systems with the shadowing property. Ergod. Th. & Dynam. Sys. 38(6) (2018), 2108–2131.CrossRefGoogle Scholar
Enrich, H., Guelman, N., Larcanché, A. and Liousse, I.. Diffeomorphisms having rotation sets with non-empty interior. Nonlinearity 22(8) (2009), 1899–1907.CrossRefGoogle Scholar
Epstein, D. B. A.. Curves on 2-manifolds and isotopies. Acta Math. 115 (1966), 83–107.10.1007/BF02392203CrossRefGoogle Scholar
Franks, J.. Realizing rotation vectors for torus homeomorphisms. Trans. Amer. Math. Soc. 311(1) (1989), 107–115.CrossRefGoogle Scholar
Franks, J. and Misiurewicz, M.. Rotation sets of toral flows. Proc. Amer. Math. Soc. 109 (1990), 243–249.10.1090/S0002-9939-1990-1021217-5CrossRefGoogle Scholar
Gromov, M.. Topological invariants of dynamical systems and spaces of holomorphic maps: I. Math. Phys. Anal. Geom. 2 (1999) 323–415.10.1023/A:1009841100168CrossRefGoogle Scholar
Guihéneuf, P.-A. and Koropecki, A.. Stability of the rotation set of area-preserving toral homeomorphisms. Nonlinearity 30 (2017), 1089–1096.CrossRefGoogle Scholar
Guihéneuf, P.-A. and Lefeuvre, T.. On the genericity of the shadowing property for conservative homeomorphisms. Proc. Amer. Math. Soc. 146 (2018), 4225–4237.CrossRefGoogle Scholar
Jenkinson, O.. Rotation, entropy, and equilibrium states. Trans. Amer. Math. Soc. 353 (2001), 3713–3739.CrossRefGoogle Scholar
Kucherenko, T. and Wolf, C.. Geometry and entropy of generalized rotation sets. Israel J. Math. 199 (2014), 791–829.CrossRefGoogle Scholar
Kucherenko, T. and Wolf, C.. Entropy and rotation sets: a toy model approach. Commun. Contemp. Math. 18(5) (2016), 1550083.CrossRefGoogle Scholar
Kwapisz, J.. Every convex polygon with rational vertices is a rotation set. Ergod. Th. & Dynam. Sys. 12 (1992), 333–339.CrossRefGoogle Scholar
Kwapisz, J.. A priori degeneracy of one-dimensional rotation sets for periodic point free torus maps. Trans. Amer. Math. Soc. 354(7) (2002), 2865–2895.CrossRefGoogle Scholar
Li, J. and Wu, M.. Points with maximal Birkhoff average oscillation. Czechoslovak Math. J. 66 (2016), 223–241.CrossRefGoogle Scholar
Lindenstrauss, E. and Tsukamoto, M.. From rate distortion theory to metric mean dimension: variational principle. Preprint, arXiv:1702.05722.Google Scholar
Lindenstrauss, E. and Weiss, B.. Mean topological dimension. Israel J. Math. 115 (2000), 1–24.CrossRefGoogle Scholar
Llibre, J. and Mackay, R.. Rotation vectors and entropy for homeomorphisms of the torus isotopic to the identity. Ergod. Th. & Dynam. Sys. 11 (1991) 115–128.CrossRefGoogle Scholar
Misiurewicz, M. and Ziemian, K.. Rotation sets for maps of tori. J. Lond. Math. Soc. 2 (1989), 490–506.CrossRefGoogle Scholar
Misiurewicz, M. and Ziemian, K.. Rotation sets and ergodic measures for torus homeomorphisms. Fund. Math. 137 (1991), 45–52.CrossRefGoogle Scholar
Newhouse, S., Palis, J. and Takens, F.. Bifurcations and stability of families of diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 57 (1983), 5–71.CrossRefGoogle Scholar
Olsen, L.. A multifractal formalism. Adv. Math. 116(1) (1995), 82–196.CrossRefGoogle Scholar
Olsen, L. and Winter, S.. Normal and non-normal points of self-similar sets and divergence points of self-similar measures. J. Lond. Math. Soc. 67 (2003), 103–122.CrossRefGoogle Scholar
Palis, J., Pugh, C., Shub, M. and Sullivan, D.. Genericity theorems in topological dynamics. Dynamical Systems – Warwick 1974 (Proc. Symp. Applied Topology and Dynamical Systems, University of Warwick, Coventry, 1973–1974) (Lecture Notes in Mathematics, 468). Springer, Berlin, 1975, pp. 241–250.Google Scholar
Passeggi, A.. Rational polygons as rotation sets of generic homeomorphisms of the two torus. J. Lond. Math. Soc. 89 (2014), 235–254.CrossRefGoogle Scholar
Pesin, Y. and Weiss, H.. The multifractal analysis of Gibbs measures: motivation, mathematical foundation, and examples. Chaos 7(1) (1997), 89–106.CrossRefGoogle ScholarPubMed
Pesin, Ya. B.. Dimension Theory in Dynamical Systems: Contemporary Views and Applications. University of Chicago Press, Chicago, IL, 1997.CrossRefGoogle Scholar
Pilyugin, S. and Plamenevskaya, O.. Shadowing is generic. Topology Appl. 97 (1999), 253–266.CrossRefGoogle Scholar
Poincaré, H.. Oeuvres completes. Tome 1. Gauthier-Villars, Paris, 1952, pp. 137–158.Google Scholar
Rees, M.. A minimal positive entropy homeomorphism of the 2-torus. J. Lond. Math. Soc. 23(3) (1981), 537–550.CrossRefGoogle Scholar
Ruelle, D.. Historical behaviour in smooth dynamical systems. Global Analysis of Dynamical Systems, Festschrift dedicated to Floris Takens for his 60th birthday. Eds. Krauskopf, B., Broer, H. and Vegter, G.. Institute of Physics, Bristol, 2001, pp. 63–66.Google Scholar
Sigmund, K.. Generic properties of invariant measures for Axiom A-diffeomorphisms. Invent. Math. 11 (1970), 99–109.CrossRefGoogle Scholar
Smale, S.. Differentiable dynamical systems. Bull. Amer. Math. Soc. 73(6) (1967), 747–817.CrossRefGoogle Scholar
Sun, P.. Minimality and gluing orbit property. Discrete Contin. Dyn. Syst. 39(7) (2019), 4041–4056.CrossRefGoogle Scholar
Takens, F.. Orbits with historic behaviour, or non-existence of averages. Nonlinearity 21(3) (2008), T33–T36.CrossRefGoogle Scholar
Takens, F. and Verbitskiy, E.. On the variational principle for the topological entropy of certain non–compact sets. Ergod. Th. & Dynam. Sys. 23(1) (2003), 317–348.CrossRefGoogle Scholar
Thompson, D.. The irregular set for maps with the specification property has full topological pressure. Dyn. Syst. 25 (2010), 25–51.CrossRefGoogle Scholar
Pesin, Ya. B. and Pitskel, B. S.. Topological pressure and the variational principle for noncompact sets. Funct. Anal. Appl. 18(4) (1984), 307–318.CrossRefGoogle Scholar
Yano, K.. A remark on the topological entropy of homeomorphisms. Invent. Math. 59 (1980), 215–220.CrossRefGoogle Scholar
Zhou, X. and Chen, E.. Multifractal analysis for the historic set in topological dynamical systems. Nonlinearity 26(7) (2013), 1975–1997.CrossRefGoogle Scholar