Article contents
On the number of fixed points of a sofic shift-flip system
Published online by Cambridge University Press: 20 August 2013
Abstract
If 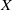 $X$ is a sofic shift and
$X$ is a sofic shift and 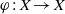 $\varphi : X\rightarrow X$ is a homeomorphism such that
$\varphi : X\rightarrow X$ is a homeomorphism such that 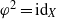 ${\varphi }^{2} = {\text{id} }_{X} $ and
${\varphi }^{2} = {\text{id} }_{X} $ and 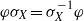 $\varphi {\sigma }_{X} = { \sigma }_{X}^{- 1} \varphi $, the number of points in
$\varphi {\sigma }_{X} = { \sigma }_{X}^{- 1} \varphi $, the number of points in 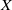 $X$ that are fixed by
$X$ that are fixed by 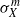 ${ \sigma }_{X}^{m} $ and
${ \sigma }_{X}^{m} $ and 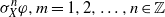 ${ \sigma }_{X}^{n} \varphi , m= 1, 2, \ldots , n\in \mathbb{Z} $, is expressed in terms of a finite number of square matrices: the matrices are obtained from Krieger’s joint state chain of a sofic shift which is conjugate to
${ \sigma }_{X}^{n} \varphi , m= 1, 2, \ldots , n\in \mathbb{Z} $, is expressed in terms of a finite number of square matrices: the matrices are obtained from Krieger’s joint state chain of a sofic shift which is conjugate to 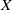 $X$.
$X$.
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2013
References
- 2
- Cited by


