Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-04T21:32:00.393Z Has data issue: false hasContentIssue false
  • English
  • Français

On the existence of non-trivial homoclinic classes

Published online by Cambridge University Press:  01 October 2007

CHRISTIAN BONATTI ,
SHAOBO GAN  and
LAN WEN
CHRISTIAN BONATTI
Affiliation:
IMB, UMR 5584 du CNRS, BP 47870, 21078 Dijon Cedex, France (email: [email protected])
SHAOBO GAN
Affiliation:
LMAM, School of Mathematical Sciences, Peking University, Beijing 100871, China (email: [email protected], [email protected])
LAN WEN
Affiliation:
LMAM, School of Mathematical Sciences, Peking University, Beijing 100871, China (email: [email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

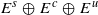We show that, for C1-generic diffeomorphisms, every chain recurrent class C that has a partially hyperbolic splitting with dimEc=1 either is an isolated hyperbolic periodic orbit, or is accumulated by non-trivial homoclinic classes. We also prove that, for C1-generic diffeomorphisms, any chain recurrent class that has a dominated splitting 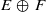with dim(E)=1 either is a homoclinic class, or the bundle E is uniformly contracting. As a corollary we prove in dimension three a conjecture of Palis, which announces that any C1-generic diffeomorphism is either Morse–Smale, or has a non-trivial homoclinic class.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 27 , Issue 5 , October 2007 , pp. 1473 - 1508
Copyright
Copyright © Cambridge University Press 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Birkhoff, G.. Dynamical Systems. American Mathematical Society, Providence, RI, 1966.Google Scholar
[2]Bonatti, C. and Crovisier, S.. Récurrence et généricité. Invent. Math. 158(1) (2004), 33–104.CrossRefGoogle Scholar
[3]Carballo, C., Morales, C. and Pacifico, M. J.. Maximal transitive sets with singularities for generic C1 vector fields. Bol. Soc. Brasil. Mat. (N.S.) 31(3) (2000), 287–303.CrossRefGoogle Scholar
[4]Conley, C.. Isolated Invariant Sets and the Morse Index (CBMS Regional Conference Series in Mathematics, 38). American Mathematical Society, Providence, RI, 1978.CrossRefGoogle Scholar
[5]Crovisier, S.. Periodic orbits and chain-transitive sets of C 1-diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 104 (2006), 87–141.CrossRefGoogle Scholar
[6]Gan, S. and Wen, L.. Heteroclinic cycles and homoclinic closures for generic diffeomorphisms. J. Dynam. Differential Equations 15 (2003), 451–471.CrossRefGoogle Scholar
[7]Gourmelon, N.. Adapted metric for dominated splitting. Ergod. Th. & Dynam. Sys. to appear.Google Scholar
[8]Hirsch, M., Pugh, C. and Shub, M.. Invariant Manifolds (Lecture Notes in Mathematics, 583). Springer, New York, 1977.CrossRefGoogle Scholar
[9]Liao, S. T.. Obstruction sets (II). Acta Sci. Natur. Univ. Pekinensis 2 (1981), 1–36.Google Scholar
[10]Mañé, R.. An ergodic closing lemma. Ann. of Math. (2) 116 (1982), 503–540.CrossRefGoogle Scholar
[11]Morales, C. and Pacifico, M. J.. Lyapunov stability of ω-limit sets. Discrete Contin. Dyn. Syst. 8(3) (2002), 671–674.CrossRefGoogle Scholar
[12]Pliss, V. A.. On a conjecture of Smale. Differ. Uravn. 8 (1972), 268–282.Google Scholar
[13]Poincaré, H.. Les Méthodes Nouvelles de la Mécanique Céleste, 3 vols. Gauthier-Villars, Paris, 1899.Google Scholar
[14]Pugh, C.. The C 1-closing lemma. Amer. J. Math. 89 (1967), 956–1009.CrossRefGoogle Scholar
[15]Pujals, E. and Sambarino, M.. Homoclinic tangencies and hyperbolicity for surface diffeomorphisms. Ann. of Math. (2) 151(3) (2000), 961–1023.CrossRefGoogle Scholar
[16]Robinson, C.. Dynamical Systems. Stability, Symbolic Dynamics, and Chaos, 2nd edn(Studies in Advanced Mathematics). CRC Press, Boca Raton, FL, 1999.Google Scholar
[17]Wen, L.. Homoclinic tangencies and dominated splittings. Nonlinearity 15 (2002), 1445–1469.CrossRefGoogle Scholar
[18]Wen, L.. Generic diffeomorphisms away from homoclinic tangencies and heterodimensional cycles. Bull. Braz. Math. Soc. (N.S.) 35(3) (2004), 419–452.CrossRefGoogle Scholar