Published online by Cambridge University Press: 11 February 2015
In this paper we consider diffeomorphisms preserving hyperbolic Sinaĭ–Ruelle–Bowen (SRB) probability measures 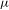 ${\it\mu}$ having intersections for almost every pair of the stable and unstable manifolds. In this context, when the dimension of the unstable manifold is constant almost everywhere, we show the ergodicity of
${\it\mu}$ having intersections for almost every pair of the stable and unstable manifolds. In this context, when the dimension of the unstable manifold is constant almost everywhere, we show the ergodicity of 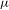 ${\it\mu}$. As an application we obtain another proof of the ergodicity of a hyperbolic SRB measure for transitive surface diffeomorphisms, which is shown by Rodriguez Hertz, Rodriguez Hertz, Tahzibi and Ures [Uniqueness of SRB measures for transitive diffeomorphisms on surfaces. Comm. Math. Phys.306(1) (2011), 35–49].
${\it\mu}$. As an application we obtain another proof of the ergodicity of a hyperbolic SRB measure for transitive surface diffeomorphisms, which is shown by Rodriguez Hertz, Rodriguez Hertz, Tahzibi and Ures [Uniqueness of SRB measures for transitive diffeomorphisms on surfaces. Comm. Math. Phys.306(1) (2011), 35–49].