Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T14:42:56.170Z Has data issue: false hasContentIssue false
  • English
  • Français

On the equidistribution of unstable curves for pseudo-Anosov diffeomorphisms of compact surfaces

Part of: Ergodic theory Dynamical systems with hyperbolic behavior Smooth dynamical systems: general theory

Published online by Cambridge University Press:  07 December 2021

GIOVANNI FORNI
GIOVANNI FORNI*
Affiliation:
Department of Mathematics, University of Maryland, College Park, MD, USA
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that the asymptotics of ergodic integrals along an invariant foliation of a toral Anosov diffeomorphism, or of a pseudo-Anosov diffeomorphism on a compact orientable surface of higher genus, is determined (up to a logarithmic error) by the action of the diffeomorphism on the cohomology of the surface. As a consequence of our argument and of the results of Giulietti and Liverani [Parabolic dynamics and anisotropic Banach spaces. J. Eur. Math. Soc. (JEMS)21(9) (2019), 2793–2858] on horospherical averages, toral Anosov diffeomorphisms have no Ruelle resonances in the open interval 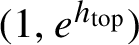$(1, e^{h_{\mathrm {top}}})$ .

Keywords

Anosov diffeomorphismsdeviation of ergodic averages for invariant foliationsRuelle asymptotics

MSC classification

Primary: 37D20: Uniformly hyperbolic systems (expanding, Anosov, Axiom A, etc.)
Secondary: 37A25: Ergodicity, mixing, rates of mixing 37C30: Zeta functions, (Ruelle-Frobenius) transfer operators, and other functional analytic techniques in dynamical systems
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 3: Anatole Katok Memorial Issue Part 2: Special Issue of Ergodic Theory and Dynamical Systems , March 2022 , pp. 855 - 880
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

In memory of Anatole Katok, with admiration and gratitude

References

Baladi, V.. There are no deviations for the ergodic averages of the Giulietti–Liverani horocycle flows on the two-torus. Ergod. Th. & Dynam. Sys. doi:10.1017/etds.2021.17. Published online 18 March 2021.CrossRefGoogle Scholar
Bufetov, A.. Limit theorems for translation flows. Ann. of Math. (2) 179(2) (2014), 431–499.CrossRefGoogle Scholar
Bufetov, A. and Forni, G.. Limit theorems for horocycle flows. Ann. Sci. Éc. Norm. Supér. (4) 47(5) (2014), 851–903.CrossRefGoogle Scholar
Delecroix, V., Hubert, P. and Lelièvre, S.. Diffusion for the periodic wind-tree model. Ann. Sci. Éc. Norm. Supér. (4) 47(6) (2014), 1085–1110.CrossRefGoogle Scholar
Faure, F., Gouëzel, S. and Lanneau, E.. Ruelle spectrum of linear pseudo-Anosov maps. J. Éc. polytech. Math. 6 (2019), 811–877.CrossRefGoogle Scholar
Forni, G.. Deviation of ergodic averages for area-preserving flows on surfaces of higher genus. Ann. of Math. (2) 155(1) (2002), 1–103.CrossRefGoogle Scholar
Forni, G.. Sobolev regularity of solutions of the cohomological equation. Ergod. Th. & Dynam. Sys. 41 (2021), 685–789.CrossRefGoogle Scholar
Forni, G. and Kanigowski, A.. Time-changes of Heisenberg nilflows. Some Aspects of the Theory of Dynamical Systems: A Tribute to Jean-Christophe Yoccoz (Astérisque, 416). Vol. II. Eds. Crovisier, S., Krikorian, R., Matheus, C. and Senti, S.. Société Mathématique de France, Paris, 2020, pp. 253–299.CrossRefGoogle Scholar
Gerber, M. and Katok, A.. Smooth models of pseudo-Anosov maps. Ann. Sci. Éc. Norm. Supér. (4) 15 (1982), 173–204.CrossRefGoogle Scholar
Giulietti, P. and Liverani, C.. Parabolic dynamics and anisotropic Banach spaces. J. Eur. Math. Soc. (JEMS) 21(9) (2019), 2793–2858.CrossRefGoogle Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems (Encyclopedia of Mathematics and Its Applications, 54). Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Marmi, S. and Yoccoz, J.-C.. Hölder regularity of the solutions of the cohomological equation for Roth type interval exchange maps. Comm. Math. Phys. 344(1) (2016), 117–139.CrossRefGoogle Scholar
Veconi, D.. Thermodynamics of smooth models of pseudo-Anosov homeomorphisms. Ergod. Th. & Dynam. Sys. doi:10.1017/etds.2021.43. Published 18 May 2021.CrossRefGoogle Scholar
Yoccoz, J.-C.. Interval exchange maps and translation surfaces. Homogeneous Flows, Moduli Spaces and Arithmetic (Clay Mathematics Proceedings, 10). American Mathematical Society, Providence, RI, 2010, pp. 1–69.Google Scholar