Article contents
On the distribution of orbits in affine varieties
Published online by Cambridge University Press: 03 July 2014
Abstract
Given an affine variety 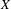 $X$, a morphism
$X$, a morphism 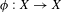 ${\it\phi}:X\rightarrow X$, a point
${\it\phi}:X\rightarrow X$, a point 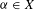 ${\it\alpha}\in X$, and a Zariski-closed subset
${\it\alpha}\in X$, and a Zariski-closed subset  $V$ of
$V$ of 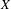 $X$, we show that the forward
$X$, we show that the forward 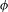 ${\it\phi}$-orbit of
${\it\phi}$-orbit of  ${\it\alpha}$ meets
${\it\alpha}$ meets  $V$ in at most finitely many infinite arithmetic progressions, and the remaining points lie in a set of Banach density zero. This may be viewed as a weak asymptotic version of the dynamical Mordell–Lang conjecture for affine varieties. The results hold in arbitrary characteristic, and the proof uses methods of ergodic theory applied to compact Berkovich spaces.
$V$ in at most finitely many infinite arithmetic progressions, and the remaining points lie in a set of Banach density zero. This may be viewed as a weak asymptotic version of the dynamical Mordell–Lang conjecture for affine varieties. The results hold in arbitrary characteristic, and the proof uses methods of ergodic theory applied to compact Berkovich spaces.
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2014
References
- 5
- Cited by


