Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T00:44:21.601Z Has data issue: false hasContentIssue false
  • English
  • Français

On the classification of Markov chains by finite equivalence

Published online by Cambridge University Press:  19 September 2008

William Parry  and
Selim Tuncel
William Parry
Affiliation:
Mathematics Institute, University of Warwick, Coventry CVA 1AL, England
Selim Tuncel
Affiliation:
Mathematics Institute, University of Warwick, Coventry CVA 1AL, England
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

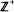We consider a certain analytic function β (t) which is an invariant of finite equivalence between two finite state Markov chains. If two such chains P, Q have the same β-function we wish to prove that they are finitely equivalent. To this end we show that U(t)Pt = QtU (t) has a nontrivial matrix solution U over the ring (exp) of integral combinations of exponential functions. In fact we can force U(t) to be strictly positiveat any specified t0. If U(t) has entries from 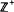(exp), the sub-semi-ring of positive integral combinations of exponential functions, then P, Q are finitely equivalent. Many examples reinforce the conjecture that U(t) may always be chosen over 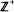(exp) when P, Q have the same β-function. We relate the β-function to topological entropy, measure entropy and information variance.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 1 , Issue 3 , September 1981 , pp. 303 - 335
Copyright
Copyright © Cambridge University Press 1981

References

REFERENCES

[1]Adler, R. L. & Marcus, B.. Topological entropy and equivalence ofdynamical systems. Mem. A.M.S. 219 (1979).Google Scholar
[2]Bhatia, R. & Mukherjea, K. K.. On the rate of change of spectra of operators. Linear Algebra and its Appl. 27 (1979), 147–157.Google Scholar
[3]Coven, E. M. & Paul, M. E.. Endomorphisms of irreducible subshifts of finite type. Math. Syst. Theory 8 (1974), 167–175.Google Scholar
[4]Fellgett, R. & Parry, W.. Endomorphisms of a Lebesgue space II. Bull. L.M.S. 7 (1975), 151–158.Google Scholar
[5]Hedlund, G. A.. Endomorphisms and automorphisms of the shift dynamical system. Math. Syst. Theory 3 (1969), 320–375.Google Scholar
[6]Parry, W.. Endomorphisms of a Lebesgue space III. Israel J. Math. 21 (1975), 167–172.Google Scholar
[7]Parry, W.. A finitary classification of topological Markov chains and sofic systems. Bull L.M.S. 9 (1977), 86–92.Google Scholar
[8]Parry, W.. University of Warwick lecture notes.Google Scholar
[9]Parry, W. & Schmidt, K.. A note on cocycles of unitary representations. Proc. A.M.S. 55 (1976), 185–190.Google Scholar
[10]Parry, W. & Williams, R. F.. Block coding and a zeta function for finite Markov chains. Proc. L.M.S. 35 (1977), 483–495.CrossRefGoogle Scholar
[11]Rosenblatt, M.. Independence and dependence. Proc. 4th Berkeley Symp. Math. Stats, and Prob. Vol. II, pp. 431–443.Google Scholar
[12]Ruelle, D.. Thermodynamic Formalism. Addison-Wesley: Reading, Mass., 1978.Google Scholar
[13]Seneta, E.. Non-negative Matrices. Allen and Unwin: London, 1973.Google Scholar
[14]Tuncel, S.. Conditional pressure and coding. Israel J. Math. 39 (1981), 101–112.CrossRefGoogle Scholar
[15]Williams, R. F.. Classification of subshifts of finite type. Ann. Math. 98 (1973), 120–153;Google Scholar
Errata. Ann. Math. 99 (1974), 380–381.Google Scholar
[16]Zariski, O. & Samuel, P.. Commutative Algebra, Vol. 1. Springer-Verlag: Berlin, 1958.Google Scholar