Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T14:37:47.805Z Has data issue: false hasContentIssue false
  • English
  • Français

On subshifts with slow forbidden word growth

Part of: Topological dynamics Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  12 January 2021

RONNIE PAVLOV
RONNIE PAVLOV*
Affiliation:
Department of Mathematics, University of Denver, 2390 S. York St., Denver, CO80208, USA (www.math.du.edu/~rpavlov/)
*
e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

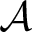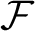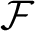In this work, we treat subshifts, defined in terms of an alphabet $\mathcal {A}$ and (usually infinite) forbidden list $\mathcal {F}$ , where the number of n-letter words in $\mathcal {F}$ has ‘slow growth rate’ in n. We show that such subshifts are well behaved in several ways; for instance, they are boundedly supermultiplicative in the sense of Baker and Ghenciu [Dynamical properties of S-gap shifts and other shift spaces. J. Math. Anal. Appl.430(2) (2015), 633–647] and they have unique measures of maximal entropy with the K-property and which satisfy Gibbs bounds on large (measure-theoretically) sets. The main tool in our proofs is a more general result, which states that bounded supermultiplicativity and a sort of measure-theoretic specification property together imply uniqueness of the measure of maximum entropy and our Gibbs bounds. We also show that some well-known classes of subshifts can be treated by our results, including the symbolic codings of 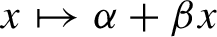$x \mapsto \alpha + \beta x$ (the so-called 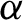$\alpha $ -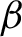 $\beta $ shifts of Hofbauer [Maximal measures for simple piecewise monotonic transformations. Z. Wahrsch. verw. Geb.52(3) (1980), 289–300]) and the bounded density subshifts of Stanley [Bounded density shifts. Ergod. Th. & Dynam. Sys.33(6) (2013), 1891–1928].

Keywords

Gibbs boundsintrinsic ergodicitysymbolic dynamics

MSC classification

Primary: 37B10: Symbolic dynamics
Secondary: 37B40: Topological entropy 37D35: Thermodynamic formalism, variational principles, equilibrium states
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 4 , April 2022 , pp. 1487 - 1516
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Baker, S. and Ghenciu, A. E.. Dynamical properties of $S$ -gap shifts and other shift spaces. J. Math. Anal. Appl. 430(2) (2015), 633–647.CrossRefGoogle Scholar
Bowen, R.. Some systems with unique equilibrium states. Math. Syst. Theory 8(3) (1974–1975), 193–202.CrossRefGoogle Scholar
Buzzi, J.. Subshifts of quasi-finite type. Invent. Math. 159(2) (2005), 369–406.CrossRefGoogle Scholar
Carapezza, L., López, M. and Robertson, D.. Unique equilibrium states for some intermediate beta transformations, submitted.Google Scholar
Climenhaga, V. and Thompson, D. J.. Intrinsic ergodicity beyond specification: $\beta$ -shifts, $S$ -gap shifts, and their factors. Israel J. Math. 192(2) (2012), 785–817.CrossRefGoogle Scholar
Climenhaga, V. and Thompson, D. J.. Equilibrium states beyond specification and the Bowen property. J. Lond. Math. Soc. (2) 87(2) (2013), 401–427.CrossRefGoogle Scholar
Climenhaga, V. and Thompson, D. J.. Intrinsic ergodicity via obstruction entropies. Ergod. Th. & Dynam. Sys. 34(6) (2014), 1816–1831.CrossRefGoogle Scholar
Gan, S.. Sturmian sequences and the lexicographic world. Proc. Amer. Math. Soc. 129(5) (2001), 1445–1451.CrossRefGoogle Scholar
García-Ramos, F. and Pavlov, R.. Extender sets and measures of maximal entropy for subshifts. J. Lond. Math. Soc. (2) 100(3) (2019), 1013–1033.CrossRefGoogle Scholar
Glendinning, P.. Topological conjugation of Lorenz maps by $\beta$ -transformations. Math. Proc. Cambridge Philos. Soc. 107(2) (1990), 401–413.CrossRefGoogle Scholar
Gurevich, B. M.. Stationary random sequences of maximal entropy. Multicomponent Random Systems (Advances in Probability & Related Topics, 6). Dekker, New York, NY, 1980, pp. 327–380.Google Scholar
Hofbauer, F.. On intrinsic ergodicity of piecewise monotonic transformations with positive entropy. Israel J. Math. 34(3) (1979), 213–237.CrossRefGoogle Scholar
Hofbauer, F.. Maximal measures for simple piecewise monotonic transformations. Z. Wahrsch. verw. Geb. 52(3) (1980), 289–300.CrossRefGoogle Scholar
Kerr, D. and Li, H.. Independence in topological and ${C}^{\ast }$ -dynamics. Math. Ann. 338(4) (2007), 869–926.CrossRefGoogle Scholar
Konieczny, J., Kupsa, M. and Kwietniak, D.. Arcwise connectedness of the set of ergodic measures of hereditary shifts. Proc. Amer. Math. Soc. 146(8) (2018), 3425–3438.CrossRefGoogle Scholar
Kułaga-Przymus, J., Lemańczyk, M. and Weiss, B.. Hereditary subshifts whose simplex of invariant measures is Poulsen. Ergodic Theory, Dynamical Systems, and the Continuing Influence of John C. Oxtoby (Contemporary Mathematics, 678). American Mathematical Society, Providence, RI, 2016, pp. 245–253.CrossRefGoogle Scholar
Kwietniak, D.. Topological entropy and distributional chaos in hereditary shifts with applications to spacing shifts and beta shifts. Discrete Contin. Dyn. Syst. 33(6) (2013), 2451–2467.CrossRefGoogle Scholar
Ledrappier, F.. Mesures d’équilibre d’entropie complètement positive. Astérisque 50 (1977), 251–272.Google Scholar
Li, B., Sahlsten, T. and Samuel, T.. Intermediate $\beta$ -shifts of finite type. Discrete Contin. Dyn. Syst. 36(1) (2016), 323–344.CrossRefGoogle Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Miller, J. S.. Two notes on subshifts. Proc. Amer. Math. Soc. 140(5) (2012), 1617–1622.CrossRefGoogle Scholar
Pavlov, R.. On controlled specification and uniqueness of the equilibrium state in expansive systems. Nonlinearity 32(7) (2019), 2441–2466.CrossRefGoogle Scholar
Pavlov, R.. On entropy and intrinsic ergodicity of coded subshifts. Proc. Amer. Math. Soc. 148(11) (2020), 4717–4731.CrossRefGoogle Scholar
Pliss, V. A.. On a conjecture of Smale. Differ. Uravn. 8 (1972), 268–282.Google Scholar
Stanley, B.. Bounded density shifts. Ergod. Th. & Dynam. Sys. 33(6) (2013), 1891–1928.CrossRefGoogle Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79). Springer, New York, 1982.Google Scholar