Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-01-10T02:48:35.088Z Has data issue: false hasContentIssue false
  • English
  • Français

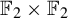On sofic approximations of ${\mathbb F}_2\times {\mathbb F}_2$

Part of: Special aspects of infinite or finite groups Permutation groups

Published online by Cambridge University Press:  04 May 2021

ADRIAN IOANA
ADRIAN IOANA*
Affiliation:
Department of Mathematics, University of California San Diego, 9500 Gilman Drive, La Jolla, CA92093, USA
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We construct a sofic approximation of 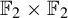${\mathbb F}_2\times {\mathbb F}_2$ that is not essentially a ‘branched cover’ of a sofic approximation by homomorphisms. This answers a question of L. Bowen.

Keywords

sofic groupsofic approximationproperty taugroup stability

MSC classification

Primary: 20B07: General theory for infinite groups
Secondary: 20F69: Asymptotic properties of groups
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 7 , July 2022 , pp. 2333 - 2351
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alon, N., Lubotzky, A. and Widgerson, A.. Semi-direct product in groups and zig-zag product in graphs: connections and applications (extended abstract). Proc. 42nd IEEE Symp. on Foundations of Computer Science (Las Vegas, NV, 2001). IEEE Computer Society, Los Alamitos, CA, 2001, pp. 630–637.Google Scholar
Arzhantseva, G. and Paunescu, L.. Almost commuting permutations are near commuting permutations. J. Funct. Anal. 269(3) (2015), 745–757.CrossRefGoogle Scholar
Bowen, L.. Examples in the entropy theory of countable group actions. Ergod. Th. & Dynam. Sys. 40(10) (2020), 2593–2680.CrossRefGoogle Scholar
Bowen, L.. A brief introduction to sofic entropy theory. Proc. Int. Congress of Mathematicians (Rio de Janeiro, 2018). Vol. 2. World Scientific, Hackensack, NJ, 2019, pp. 1847–1866.CrossRefGoogle Scholar
Bourgain, J. and Varjú, P.. Expansion in SLd (ℤ/qℤ), q arbitrary. Invent. Math. 188(1) (2012), 151–173.CrossRefGoogle Scholar
Elek, G. and Szabó, E.. Sofic representations of amenable groups. Proc. Amer. Math. Soc. 139 (2011), 4285–4291.CrossRefGoogle Scholar
Ioana, A.. Compact actions whose orbit equivalence relations are not profinite. Adv. Math. 354 (2019), 106753, 19 pp.CrossRefGoogle Scholar
Ioana, A.. Stability for product groups and propert (τ). J. Funct. Anal. 279(9) (2020), 108729.CrossRefGoogle Scholar
Lazarovich, N., Levit, A. and Minsky, Y.. Surface groups are flexibly stable. Preprint, 2019, arXiv:1901.07182.Google Scholar
Lubotzky, A. and Segal, D.. Subgroup Growth (Progress in Mathematics, 212). Birkhäuser, Basel, 2003.CrossRefGoogle Scholar
Lubotzky, A.. Discrete Groups, Expanding Graphs and Invariant Measures (Progress in Mathematics, 125). Birkhäuser, Basel, 1994. With an Appendix by Jonathan D. Rogawski.CrossRefGoogle Scholar
Arzhantseva, G., Thom, A. and Valette, A.. Finite-dimensional approximation of discrete groups. Oberwolfach Rep. 8(2) (2011), 1429–1467 (English summary). Abstracts from the workshop held on May 15–21, 2011.CrossRefGoogle Scholar
Thom, A.. Finitary approximations of groups and their applications. Proc. Int. Congress of Mathematics (Rio de Janeiro, 2018). Vol. 2. World Scientific, Hackensack, NJ, 2019, pp. 1775–1796.Google Scholar